Question 455735: If V={v1,v2,...,vk} is linearly independent, and w is not element of V. Then show that {v1+w,v2+w,...,vk+w} is linearly independent
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let  +...+ +...+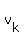 . .
Now let
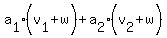 +...+ +...+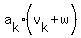 = =  , ,
which for the purpose of contradiction, we assume that not all the a's are 0, (i.e., the set is linearly DEPENDENT).
==> (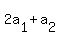 +...+ +...+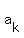 )* )*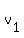
+(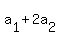 +...+ +...+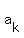 )* )*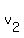 + ...+( + ...+(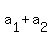 +...+ +...+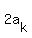 )* )*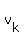 = = 
By the hypothesis, {v1, v2, v3,..., vk } is linearly independent, and thus,
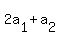 +...+ +...+
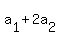 +...+ +...+
...................................
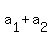 +...+ +...+ . .
We get a homogeneous system of equations.
Adding all corresponding sides of the system, we get
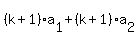 +...+ +...+
OR,
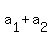 +...+ +...+ . .
Subtracting this equation from each one of the equations in the system above, we obtain
 =...= =...= , ,
CONTRARY to the initial assumption that not all a's are 0.
Hence {v1+w,v2+w,...,vk+w} must be linearly independent.
|
|
|