SOLUTION: Solve the following system of nonlinear equations 25x^2+9y^2=225 x-y=0

I'll do it first graphically and then I'll do it algebraically. 


The first equation has x intercepts (-3,0), (3,0). 
It also has y-intercepts (0,5), (0,-5), so it is this ellipse.

 

The second equation is of this line:

 

Putting them on the same set of axes:

 

If we draw lines to the axes from the points of intersections



It appears that the two points of intersection are (2.6,2.6)

and (-2.6,-2.6)

Now we'll do it algebraically to find the points exactly:



Use substitution.  Solve the second equation for y



So we substitute x for y is the first equation:















And since 

The points of intersection (exact values) are:

(x,y) = (, )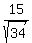

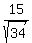(x,y) = (, ) 

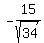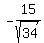The decimal approximations are:

(x,y) = (2.572478777, 2.572478777)

(x,y) = (-2.572478777, -2.572478777)

Edwin