SOLUTION: Can you find the coordinates of B given A(3,8) and M(5,4)? M is the midpoint of. Graph: A-----M-----B

There are two ways.  We'll do both.

Graphically:

  

Draw the right triangle with one leg vertical and one leg 
horizontal that has AM as its hypotenuse:



Notice that the vertical leg is 4 units and the horizontal leg is 2 units
long.  So duplicate that triangle below, and you have this, so you see that
M(5,4) is the midpoint between A(3,8) and B(7,0).



Second way:

Let B have the coordinates B(, )

Then use the midpoint formula:

Midpoint between (,) and  (, )

is 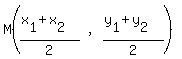  = (5,4)

Let A(3,8) = (,)

so that , and 

Let B have the coordinates B(, )

Then  



and



So you have the system of equations



Multiply both equations through by 2



Solve each and get:



So M(5,4) is the midpoint between A(3,8) and B(7,0).

Do it whichever way your teacher wants.

Edwin