The original problem was
Maximize 
subject to
Then slack variables were 
, 
, 
were
introduced to turn the inequalities into equations and the
objective function equation rearranged at the bottom with 0 on
the right side:
Then it was written as
And this system of equations was written as an augmented matrix:
The most negative number (indicator) on the bottom row is -3.
It is in column 1, so column 1 is the PIVOT COLUMN
We now divide each of the positive numbers above -3 INTO the
element at the far right of its row:
5 15
2)10 1)15
The smallest of 5 and 15 is 5, which was gotten using the elements
of row 1, so row 1 is the PIVOT ROW.
So the element in the PIVOT ROW and the PIVOT COLUMN is the 2,
which is called the PIVOT ELEMENT.
We make the pivot element into a 1 by dividing the entire pivot row through
by 2.
Now we make all the other numbers in the pivot colomn 0 by using this
pivot row, multipling it by whatever is necessary to multiply it by so
that when we add it to the other row its first element will be 0.
We make the 1 in the 2nd row 1st column a 0 by multiplying the 1st
row temporarily by -1 and adding it to row 2.
We make the -3 in the 3rd row 1st column a 0 by multiplying the 1st
row temporarily by 3 and adding it to row 3.
Now there are no more negative numbers on the bottom row. So we
write the matrix as a system of equations:
Eliminate the zero terms and the 1 coefficients:
Now solve the bottom equation for z, the letter to maximize:
Since 
, 
, and are non-negative,
the maximum value z can take on is 15, when , ,
and are all 0, so we substitute 0 for ,
, and
and the system becomes:
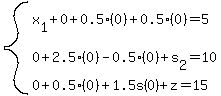or
So z reaches the maximum value of 
when
, 
, and 
. And
of course the slack variables 
and 
.
Edwin
