SOLUTION: a+b+c+d+e+f=0 a-2b=0 a+2b+3d+2e=220 1+3c+2d+2f=110 a+2b+4d+e+5f=240 a+2d+3e+4f=165 *write the equations in matrix form AX=B. *using an appropriate software package find

Algebra ->  College  -> Linear Algebra -> SOLUTION: a+b+c+d+e+f=0 a-2b=0 a+2b+3d+2e=220 1+3c+2d+2f=110 a+2b+4d+e+5f=240 a+2d+3e+4f=165 *write the equations in matrix form AX=B. *using an appropriate software package find       Log On


   

Question 251271: a+b+c+d+e+f=0
a-2b=0
a+2b+3d+2e=220
1+3c+2d+2f=110
a+2b+4d+e+5f=240
a+2d+3e+4f=165
*write the equations in matrix form AX=B.
*using an appropriate software package find the inverse of A.
*solve the above equations using the Matrix Inverse Method.
*check your answer using Cramer's rule and the Gaussian Elimination Method.
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!

I think you must have mistyped the equation 

1+3c+2d+2f=110

as none of the others had a number in front
that you had to subtract from both sides, so
if the answer I get is not the right one it's
because you mistyped that 1 in front of the 
fourth equation

a+b+c+d+e+f=0
a-2b=0
a+2b+3d+2e=220
1+3c+2d+2f=110
a+2b+4d+e+5f=240
a+2d+3e+4f=165 

1a + 1b + 1c + 1d + 1e + 1f =   0
1a - 2b + 0c + 0d + 0e + 0f =   0
1a + 2b + 0c + 3d + 2e + 0f = 220
0a + 0b + 3c + 2d + 0e + 2f = 110-1
1a + 2b + 0c + 4d + 1e + 5f = 240
1a + 0b + 0c + 2d + 3e + 4f = 165

Simplifying the equation that I think
you mistyped:

1a + 1b + 1c + 1d + 1e + 1f =   0
1a - 2b + 0c + 0d + 0e + 0f =   0
1a + 2b + 0c + 3d + 2e + 0f = 220
0a + 0b + 3c + 2d + 0e + 2f = 109
1a + 2b + 0c + 4d + 1e + 5f = 240
1a + 0b + 0c + 2d + 3e + 4f = 165 

This is the matrix AX=B form:

 

The inverse of that matrix is:



We multiply both sides of the AX=B equation by that
inverse matrix, getting it in the form A%5E%28-1%29%28AX%29=A%5E%28-1%29B

 

Matrix multiplication. though not commutative, is
associative, so we move the parentheses and change the
A%5E%28-1%29%28AX%29=A%5E%28-1%29B form to the
%28A%5E%28-1%29A%29X=A%5E%28-1%29B form



Next we do the matrix multiplication on both sides, and
since A%5E%28-1%29%2AA=I we have the IX=A%5E%28-1%29B form:



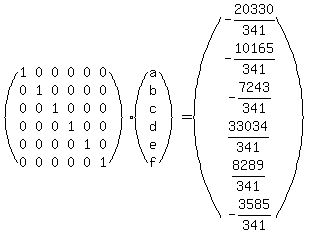When we make the multiplication on the left, we
have the final solution, the X=A%5E%28-1%29B form:



The answer you wanted is probably all different numbers since you 
probably mistyped that 1 in front of the 4th equation instead of
what it should have been.

I did the above on a TI-84 calculator.

Edwin