Question 199856: (s") + 6s' - 9s = t^2
where s" is like
d^2x/dt^2
(s") + 6s' - 9s = t^2
where s" is like
d^2x/dt^2
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a 2nd order linear differential equation. So here are the steps to finding the general solution:
Step 1) Find the complementary solution 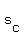
Solve the characteristic equation  to get to get  or or  . Since we have two unique real roots, this means that the complementary solution is . Since we have two unique real roots, this means that the complementary solution is 
Note: recall, if you have two real roots  and and  of the characteristic equation, then the complementary solution is of the characteristic equation, then the complementary solution is 
Step 2) Find the operator that annihilates the right hand side 
The operator  annihilates annihilates  , ,  , and , and 
We can rewrite the given differential equation as: 
When we apply the operator  to both sides, we get: to both sides, we get: 
Because  annihilates annihilates  , ,  , and , and  , we know that the particular solution , we know that the particular solution 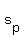 is is

Derive 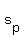 to get: to get:

Derive again to get:

Now plug this information into the original differential equation to get



So this means that



Solve the system above to get  , ,  , and , and 
So the particular solution is 
This means that the general solution is

Plug in 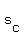 and and 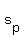 (what we found earlier) to get: (what we found earlier) to get:

So that is the final answer.
Note: there is another way to solve this problem, but it involves nasty integrals. Even though there's a lot going on here, the solution method is really straightforward.
|
|
|