Question 17949: I have been working on trying to find the eigenvalues and eigenvectors of the following matrix:
3 -1 2
2 0 2
5 -1 0
I have worked it to the point of finding the characteristic polynomial of:
-Lambda^3 + 3*Lambda^2 + 10*Lambda -8
This doesn't seem correct to me since, MATLAB gives the eigenvalues of (4,-2,1).
That is where I am stuck.
Any help is greatly appreciated.
Answer by venugopalramana(3286)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have been working on trying to find the eigenvalues and eigenvectors of the following matrix:
3 -1 2
2 0 2
5 -1 0
I have worked it to the point of finding the characteristic polynomial of:
-Lambda^3 + 3*Lambda^2 + 10*Lambda -8
This doesn't seem correct to me since, MATLAB gives the eigenvalues of (4,-2,1).
That is where I am stuck.
**************************************************************************
ok let us check we have..(due to difficulty in depiction ,I am omitting the vertical bars to show determinant..|xx| is shown as xxx)...k is used instead of lambda)
 =0 =0
(3-k)(k^2+2)-2(k+2)+5(2k-2)=0
3k^2+6-k^3-2k-2k-4+10k-10=0
-k^3+3k^2+6k-8=0.=f(k)..we find f(1)=0..so k-1 is a factor..dividing with k-1
1...|...-1....3....6....-8
....|....0....-1...2....8
*************************************************.
.........-1...2....8....0
we get -k^2+2k+8=0
...-k^2+4k-2k+8=0
-(k-4)(k+2)=0
hence k=-2 or 4...or eigen values are 1,-2 and 4..now to find eigen vectors we have to put k=1,-2 and 4 in the matrix eqn (A-kI)(X)=0 and find the solutions
where as you know A is the given matrix,k is the eigen values we got,I is the unit matrix and X is the vector (x,y,z)
for k=1,we get (A-kI)as

hence  * *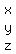 =0..or =0..or
2x-y+2z=0....(1)
2x-y+2z=0....(2)
5x-y-z=0.....(3)
(3)-(2) gives3x-3z=0...or x=z..substituting in (3) we get y=4x=4z
hence the eigen vector is 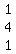 ... ...
i trust you can find the other 2 eigen vectors for k=-2 and k=4 in a similar way.
|
|
|