SOLUTION: I solved 48 problems but this one has me stumped and I have been working on it for 2hrs. Solve the following system of nonlinear equations. x^2 + y^2 = 3 x^2 + y = 0

Algebra ->  College  -> Linear Algebra -> SOLUTION: I solved 48 problems but this one has me stumped and I have been working on it for 2hrs. Solve the following system of nonlinear equations. x^2 + y^2 = 3 x^2 + y = 0      Log On


   

Question 169252: I solved 48 problems but this one has me stumped and I have been working on it for 2hrs.
Solve the following system of nonlinear equations.
x^2 + y^2 = 3
x^2 + y = 0
Found 3 solutions by Earlsdon, ankor@dixie-net.com, Edwin McCravy:
Answer by Earlsdon(6294) About Me  (Show Source):
You can put this solution on YOUR website!
Solve the system of equations:
1) x%5E2%2By%5E2+=+3 This is a circle with its center at the origin and radius of sqrt%283%29.
2) x%5E2%2By+=+0 This is a parabola that opens downard with its vertex at the origin.
Subtract equation 1) from equation 2) to get:
y%5E2-y+=+3 Subtract 3 from both sides.
y%5E2-y-3+=+0 Solve using the quadratic formula: y+=+%28-b%2B-sqrt%28b%5E2-4ac%29%29%2F2a where: a = 1, b = -1, and c = -3
y+=+%28-%28-1%29%2B-sqrt%28%28-1%29%5E2-4%281%29%28-3%29%29%29%2F2%281%29
y+=+%281%2B-sqrt%281-%28-12%29%29%29%2F2
y+=+%281%2B-sqrt%2813%29%29%2F2
y+=+%281%2Bsqrt%2813%29%29%2F2 or y+=+%281-sqrt%2813%29%29%2F2 Now substitute these values of y, one-at-a-time, into either one of the two given equations to solve for x. Let's use equation 2)
x%5E2%2By+=+0 Subtract y from both sides.
x%5E2+=+-y Substitute y+=+%281%2Bsqrt%2813%29%29%2F2
x%5E2+=+-%281%2Bsqrt%2813%29%29%2F2 Take the square root of both sides.
x+=+sqrt%28-%281%2Bsqrt%2813%29%29%2F2%29
So one solution is:
(sqrt%28-%281%2Bsqrt%2813%29%29%2F2%29,%281%2Bsqrt%2813%29%29%2F2)

Answer by ankor@dixie-net.com(22740) About Me  (Show Source):
You can put this solution on YOUR website!
Solve the following system of nonlinear equations.
x^2 + y^2 = 3
x^2 + y = 0
---------------Subtraction eliminate x^2
y^2 - y = 3
:
y^2 - y - 3 = 0
:
Solve the quadratic equation using the quadratic formula:
x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+
In this equation a=1, b=-1, c=-3
y+=+%28-%28-1%29+%2B-+sqrt%28-1%5E2+-+4%2A1%2A-3+%29%29%2F%282%2A1%29+
;
y+=+%281+%2B-+sqrt%281+-+%28-12%29+%29%29%2F%282%29+
:
y+=+%281+%2B-+sqrt%2813+%29%29%2F%282%29+
Two solutions
y+=+%281+%2B+3.6%29%2F%282%29+
y+=+4.6%2F2
y = 2.3
and
y+=+%281+-+3.6%29%2F%282%29+
y+=+-2.6%2F2
y = -1.3
:
Find x using the 2nd equation using y = +2.3
x^2 + 2.3 = 0
x^2 = -2.3
x = Sqrt(-2.3) not a real solution
:
Using y = -1.3
x^2 - 1.3 = 0
x^2 = +1.3
x = sqrt(1.3)
x = 1.14
:
Check solution in the 1st equation
1.14^2 + (-1.3^2) =
1.3 + 1.69 = 2.99 ~ 3
:
Solutions: x = 1.14, y = -1.3
;
You can check in the 2nd equation:

Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
I solved 48 problems but this one has me stumped and I have been working on it for 2hrs.
Solve the following system of nonlinear equations. 

system%28x%5E2+%2B+y%5E2+=+3%2Cx%5E2+%2B+y+=+0%29

Solve the second for y:

x%5E2%2By=0
y=-x%5E2

Substitute in the first original equation:

x%5E2%2By%5E2=3

x%5E2%2B%28-x%5E2%29%5E2=3

x%5E2%2B%28x%5E4%29=3

x%5E4%2Bx%5E2-3=0

Let x%5E2=W.  Then x%5E4=W%5E2

Substitute those:

W%5E2%2BW-3=0

This does not factor so we have to use
the quadratic formula:

W+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29+

where matrix%281%2C5%2C+++a=1%2C+%22%2C%22%2C+b=1%2C+%22%2C%22%2C+c=-3%29

W+=+%28-%281%29+%2B-+sqrt%28+%281%29%5E2-4%2A%281%29%2A%28-3%29+%29%29%2F%282%2A%281%29%29+ 

W+=+%28-1+%2B-+sqrt%281%2B12%29%29%2F2+

W+=+%28-1+%2B-+sqrt%2813%29%29%2F2+

But we do not want W.  We want x, so

since we let x%5E2=W, we have

x%5E2+=+%28-1+%2B-+sqrt%2813%29%29%2F2+  

Using the +, and the principle of
square roots:

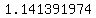x+=+%22%22%2B-sqrt%28%28-1+%2B+sqrt%2813%29%29%2F2%29 = ±1.141391974, approximately

Substituting in y=-x%5E2

y=-x%5E2

y+=+-%28-1+%2B+sqrt%2813%29%29%2F2%29+=+-1.302775638, approximately.

So we have two solutions:

(x, y) = (±1.141391974, -1.302775638)

Those are the only real solutions.  

To find the imaginary solutions,

we use the -, and the principle of
square roots:

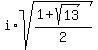x+=+%22%22%2B-sqrt%28+%28-1+-+sqrt%2813%29%29%2F2+%29++= ±i%2Asqrt%28++%281%2Bsqrt%2813%29%29%2F2+%29= ±1.517489914i, approximately.

Substituting in y=-x%5E2

y=-x%5E2

y+=+-%28-1+-+sqrt%2813%29%29%2F2%29+=+%281%2Bsqrt%2813%29%29%2F2=+2.302775638, approximately.

So we have two imaginary solutions:

(x,y) = (±1.517489914i,2.302775638)

Edwin