Question 15391: Suppose V is an n dimensional vector space and that T is an operator on V. T has n distinct eigenvalues. Also suppose that S is also an operator on V which has the same eigenvectors as T ( not necessarily with the same eigenvalues).
Prove that ST = TS
Answer by khwang(438)   (Show Source):
You can put this solution on YOUR website! Suppose V is an n dimensional vector space and that T is an operator on V. T has n distinct eigenvalues. Also suppose that S is also an operator on V which has the same eigenvectors as T ( not necessarily with the same eigenvalues).
Prove that ST = TS
Proof: If T has n distinct eigenvalues {λi| i=1,2,..,n}(i.e. 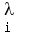 ) with corresponding eigenvectors {vi|i=1,2,..n},
then {vi|i=1,2,..n} is linear independent and so forms a basis of V.
For each i, vi is an eigenvector of S means there exists scalar βi
such that Svi = βi vi.
Consider ST (vi) = S(λi vi ) = λi S(vi) = λiβi vi and
TS (vi ) = TS (βi vi ) = βi T(vi) =λiβi vi for every i=1,2,..n.
This shows ST = TS (since {vi|i=1,2,..n} is a basis of V).
Fact. The eigenvectors {vi|i=1,2,..,n} of T is linearly independent
Proof: If 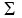  for some scalars ci,
set L to be the product operator
II(T –λj I) (j=1,2,..,n-1 ). Then, we have L(Σci vi) =Σci L(vi)
= Σci (λi vi -λi vi) (i=1,2,..,n-1) + cn II(λn -λi )vn
= cn II(λn -λi )vn = 0 .
Since all {λi} are distinct, II(λn -λi ) <> 0. (i=1,2,..,n-1)
We obtain cn = 0. Similarly, we can prove that all other scalars ci are zeros. This shows that {vi} are independent.
Kenny
PS. I don't quite believe that some questions like this would be posted
here.
|
|
|
