Question 15310: Let x1<...< xm . For I = 1,…,m, define linear operators
Ti : Pn --> R1
By Tip = p(xi). If m<=n, show that (T1,...Tm) is linearly independent. What happens if m>n? Explain
Answer by khwang(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x1<...< xm . For I = 1,…,m, define linear operators
Ti : Pn --> R1
By Tip = p(xi). If m<=n, show that (T1,...Tm) is linearly independent. What happens if m>n? Explain
Since you did not explan everything clear. No any of your work was shown.
And you posted in wrong place. I don't quite feel like to answer it.
Still .. for my weak mind
Your 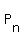 supposed to be the n -dim space of polynomials over R with degree <= n-1. Here, I use y as the variable in supposed to be the n -dim space of polynomials over R with degree <= n-1. Here, I use y as the variable in 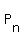 . .
Sol: Let  , i =1,2,..,n. We know that these n , i =1,2,..,n. We know that these n
polynomials form a basis of 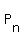 . .
If  are m distinct real numbers. are m distinct real numbers.
To show (T1,...Tm) is linearly independent. We have to show that
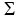  = 0 for any p in = 0 for any p in 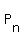 ...(*) ...(*)
implies 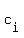 = 0 for all real number = 0 for all real number 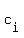 i=1,..,m i=1,..,m
When m <= n,
Chooseing p to be one of the n polynomials of the basis
 , say , say 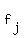 for some 1<= j<= n for some 1<= j<= n
We have 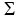 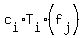 = 0 = 0
Since  } and } and 
for all i=1,2,..,m and fixed j.
We get a system of n equations of m variables 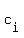 from (*) from (*)
[ Note: i summation over 1 to m ]
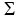 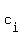 = 0 (j=1) = 0 (j=1)
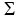 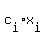 = 0 (j=2) = 0 (j=2)
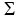 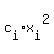 = 0 (j=3) = 0 (j=3)
...
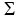 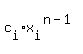 = 0 (j=n) = 0 (j=n)
This system is equivalent to the matrix equation
AX = 0, where A = (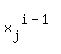 ) i=1,2,..,n, j=1,2,..,m. ) i=1,2,..,n, j=1,2,..,m.
X= (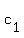 , , ,..., ,...,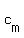 ) : mx1 column vector and 0 is nx1 matrix ) : mx1 column vector and 0 is nx1 matrix
Now consider the rank of the nxm matrix A, we know that
rank A <= min(m,n). By now A = (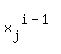 ), since all ), since all 
are distinct. Let k = min(m,n), the square kxk submatrix of A has
determinant = II (x[i] -x[j]) (i > j) , which is non-zero , so we have
rank A = min(m,n).
(e.g.
(   ) )
(  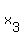 ) )
(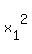 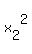 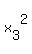 ) )
with det = (x[1] - x[2]) (x[2] - x[3])(x[3] - x[1]) <> 0 )
If m <= n, then rank(A) = m,
The linear transformation
A: 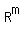 --> -->  , m = nullity (A) + rank(A) = nullity (A) + m. , m = nullity (A) + rank(A) = nullity (A) + m.
So, we have nullity(A) = 0, this means null(A) = {0}.
That is, the equation A X = 0 has unique solution of zero vector
Hence, all 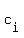 = 0 ,i=1,2,..m . = 0 ,i=1,2,..m .
This proves that (T1,...Tm) is linearly independent.
If m > n, then rank(A) = n. By m = nullity (A) + rank(A) = nullity (A) + n.
Hence, nullity (A) = m-n > 0. This means AX = 0 has nonzero solution.
Therfore, not all 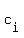 = 0 ,i=1,2,..m . = 0 ,i=1,2,..m .
This shows that (T1,...Tm) is linearly dependent if m > n.
This proof is not quite easy for beginners. Try to read carefully to
understand it.
Kenny
|
|
|