Question 15128: Let T be a linear operator on V.
Tv1= -v1-v2 and Tv2= v1-3v2 where (v1,v2) is a basis for V.
a) Find the characteristic and minimal polynomial.
b) Find all the linearly independent eigenvectors.
c) Find a jordan basis for T and exhibit the jordan form.
Answer by khwang(438)   (Show Source):
You can put this solution on YOUR website! I really cannot believe that anybody would ask questions about Jordan form,
since I know that nodbody knows much about linear algebra here.
Sol: a) T(1, 0) = (-1,-1), T(0,1) = (1,-3)
(-v1 –v2) (-1 ,–1) (v1)
(v1 –3v2) (1 ,- 3) (v2)
The matrix representation [T}B as (where B = {v1,v2} )
(-1 ,1)
(1, -3)
char(T) = det(xI –T) = (x+1)(x+3) + 1 =  ,
there is one double root: -2
So, the only eigenvalue of T is -2.
Since T + 2I =
(1 ,-1)
(1, -1) is not the zero matrix.
And we know that the minimal polynomial min(T) is a factor of char(T) so,
min(T) = char(T) =  .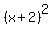
b) To find the eigenvectors(eigenspace) for the eigenvalue -2,we have to solve Tx = -2 x for nonzero vectors x.
That is, for the null space N(T+2I) of T+2I as:
Solve equations:
(1 –1) (x) (0)
(1 –1) (y) = (0), we see that x - y = 0 .
Hence, the eigenspace for the unique egenvalue–2 is <(1,1)>= {c(1,1) | c in R} (one dim. subspace generated by (1,1)). That is, the eigenspace has a basis {(1,1)}
c) Since {(1,1)} is a basis of the N(T+2I) and T+2I is not the zero vector.
Find a vector (x,y) such that (T + 2 I) (x, y) = (1,1). That is, x-y =1. Say, choose (1,0). Then, {(1,0), (1,1)} can form a Jordan basis for T and the corresponding Jordan form as
(-2 0)
(1 –2).
[Check: T(1,0) = (-2,1) = -2(1,0) + (0,1) and T(1,1) = -2(0,1) correct.]
Try to read carefully about every details and study hard.
I won't do too much for lazy students.
Kenny
PS.
By the way, since min(T) = 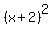, we claim that {v, (T+2I)v} can be a Jordan basis for T if v is a vector such that (T+2I)v being non-zero.(i.e v is not in Null(T+2T)) (Why ?)
This shows there are (infinitely) many Jordan basis for T.
In fact, for this example, any v = (a,b) with a <> b ,
then {v, (1,1)} can be a Jordan basis for T.
|
|
|
