please show your work on finding the inverse of the function problem


First of all, this function is not one-to-one, so its inverse would
not be a function. Here is its graph:
 To be one-to-one, a function must not only pass the vertical line
test, it also must pass the horizontal line test as well. As you
can see this graph does not pass the horizontal line test.
However we can restrict the domain in two ways, splitting the
graph into two separate parts, each of which has an inverse.
If we restrict the function to the interval (
To be one-to-one, a function must not only pass the vertical line
test, it also must pass the horizontal line test as well. As you
can see this graph does not pass the horizontal line test.
However we can restrict the domain in two ways, splitting the
graph into two separate parts, each of which has an inverse.
If we restrict the function to the interval ( ,
,  ],
we have this graph:
],
we have this graph:
 To find the inverse
To find the inverse
 Change
Change  to
to 
 Interchange x and y
Interchange x and y

 Group the
Group the 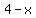
 Use the quadratic formula to solve for y:
Use the quadratic formula to solve for y:




 Now if you just take the +, you have
Now if you just take the +, you have
 Change the y to
Change the y to 
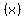

 and the graph of that is:
and the graph of that is:
 Now if you put both graphs on the same graph:
Now if you put both graphs on the same graph:
 Now if you plot the identity line
Now if you plot the identity line  , you see that, the inverse
function is the reflection of the original function across the
identity line
, you see that, the inverse
function is the reflection of the original function across the
identity line 
 You can also do the same with the right half of the original graph:
You can also do the same with the right half of the original graph:
 and the equation of that inverse function is
and the equation of that inverse function is

 Edwin
Edwin