Question 137759: Can you show that, given two equations y = m1x + c1 and y = m2x + c2 where c1 and c2 are different, there is no solution if i>m1 = m2. Interpret this result graphically. Also show that if c1 = c2 then there will be at least one solution no matter what m1 and m2 are. Interpret this result on a graph.
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two lines are parallel if and only if their slopes are equal. Since the coefficient on the x-term of a linear equation in slope intercept form is the slope of the line, if the two slopes are equal, then the lines are parallel. Since the constant term is the value of the y-coordinate of the point of intersection between the line and the y-axis, if the two constant terms are different, the two lines must intersect the y-axis in different points, hence the two parallel lines cannot be the same line. To illustrate the point graphically, draw two parallel lines. Label the points of intersection with the y-axis as (0,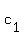 ) and (0, ) and (0, ). ).
On the other hand, if  , then regardless of the values of , then regardless of the values of 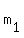 and and  , the lines will intersect at (0,b). If , the lines will intersect at (0,b). If 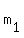 and and  happen to be equal, then the two lines are the same line and there are an infinite number of elements in the solution set. If happen to be equal, then the two lines are the same line and there are an infinite number of elements in the solution set. If 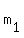 and and  are not equal, then they will intersect in just one point, namely (0,b), and that will be the single element in the solution set. To illustrate graphically, draw two lines that intersect each other and the y-axis all at the same point. Label this point (0,b) and make reference to the fact that are not equal, then they will intersect in just one point, namely (0,b), and that will be the single element in the solution set. To illustrate graphically, draw two lines that intersect each other and the y-axis all at the same point. Label this point (0,b) and make reference to the fact that  . .
|
|
|