Question 133224: I have been busting my head over a matrices problem where I need to find a pattern between the original square matrix (4, 2, 2, 4) and its exponential values.
The matrix squared is (20, 16, 16, 20) or 2(10, 8, 8, 10).
The matrix cubed is (112, 104, 104, 112) or 2(56, 52, 52, 56).
The matrix to the power of 4 is (656, 640, 640, 656) or 2(328, 320, 320, 328).
The matrix to the power of 5 is (3904, 3872, 3872, 3904) or 2(1952, 1936, 1936, 1952).
The matrix to the power of 7 is (140032, 139904, 139904, 140032) or 2(70016, 69952, 69952, 70016).
So far, what I have figured out is that the difference between the different elements in the matrices is always 2^n. As well, taking the original matrix, one can see that when k=3, the data inside the matrix is k+1 in two positions and k-1 in the other two. I can also factor out a 4 from each matrix, but that didn't seem to lead anywhere.
Can anyone help me with this emergency?
*Note: this question did not come from any textbook.
Answer by vleith(2983)   (Show Source): (Show Source):
You can put this solution on YOUR website! I don't claim to know much about matix algebra. But I do see a pattern.
To get the first of each successive row, take 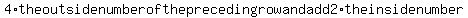 . .
To get the second number in the successive row, take 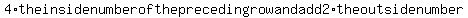
Thus, given (4,2,2,4) to get the second row,
(4*4)+(2*2), (2*4)+(4*2), (2*4)+(4*2), (4*4)+(2*2)
(20, 16, 16, 20)
To get the third row from the second row,
(4*20)+(2*16), (4*16)+(2*20), (4*16)+(2*20), (4*20)+(2*16)
(112, 104, 104, 112)
|
|
|