Question 1196602: Solve the linear programming problem.
Minimize z=4x+5y and find the ordered pairs.
Subject to
2x+y Greater than and equal to 10
X+2y Greater than and equal to 8
X,Y Greater than and equal to 0
Found 3 solutions by MathLover1, ewatrrr, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! given:
 .........1) objective function .........1) objective function
Subject to
 ........c1 ........c1
 ..........c2 ..........c2
where c1 and c2 are 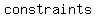
 , , ->decision variables ->decision variables
 , , >= >=  -> ->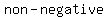 constraints constraints
first graph c1 and c2 (just positive parts in first quadrant )
 ........c1 ........c1
 | |
 | |
 | |
 ........c2 ........c2
 | |
 | |
 | |
graph them

now find the coordinates of the c1 and c2

 -> solve for -> solve for  and you have and you have 
substitute in 






then


the feasible region is above the lines around intersection point which is ( , , ) )

corner points of the feas-region are ( , , ),( ),( , , ), and ( ), and ( , , ) )
now check at which point objective function have greatest value
 .........1) check ( .........1) check ( , , ) )


 .........1) check ( .........1) check ( , , ) )


 .........1) check ( .........1) check ( , , ) )


as you can see, the maximum is at point ( , , ) )
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Minimize z=4x+5y
Subject to
2x+y >= 10
X+2y >= 8
minimum values of x & y, with x,y > 0
2x + y = 10
x + 2y = 8
2x + y = 10
-2x -4y =-16
-3y = -6
y =  and x = 8 - 4 = and x = 8 - 4 = 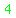 z=4x+5y minimized P(4,2)
z = 16 + 10 = 26, minimum value
Wish You the Best in your Studies.
z=4x+5y minimized P(4,2)
z = 16 + 10 = 26, minimum value
Wish You the Best in your Studies.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(1) Tutor MathLover1 tried to find the maximum value of the objective function instead of the minimum. But there is no maximum value of the objective function, because the feasibility region is unbounded.
Because the feasibility region is unbounded, it only makes sense to find the minimum value of the objective function.
(2) Tutor @ewatrrr in her response said nothing about how she decided the minimum value of the objective function was at (4,2). That is a necessary part of the solution process.
Most resources will tell you that you need to evaluate the objective function at all corners of the feasibility region to determine the minimum/maximum value of the objective function. But that is NOT true. You can determine the corner of the feasibility region where the objective function will be minimized by comparing the slope of the objective function to the slopes of the constraint boundary lines.
In this example, the constraints are
(1) 2x+y >= 10 --> y >= -2x+10
(2) x+2y >= 8 --> y >= (-1/2)x+4
The objective function is
C = 4x+5y --> y = (-4/5)x+C (I use C instead of z to make it clear that C is some constant, not a variable)
The slope of the objective function is -4/5; the minimum and maximum values of the objective function will be at the points in the feasibility region where a line with slope -4/5 just touches the feasibility region.
Since the slope of the objective function is between the slopes of the two constraint functions, the minimum value of the objective function will be where the two constraint boundary lines intersect -- at (4,2). The value of the objective function there is 4(4)+5(2) = 16+10 = 26.
NOTE: To see that the minimum value of the objective function will be at the intersection of the two constraint boundary lines, picture the graph of the two constraint boundary lines with slopes -2 and -1/2; then imagine sliding a straight edge with slope -4/5 up and down in the picture. Because its slope is between the slopes of the two constraint boundary lines, it will just touch the feasibility region at the intersection of those constraint boundary lines.
ANSWER: The minimum value of the objective function is 26, at (4,2).
|
|
|