Question 1190667: For which value of 𝑎 does each of the following systems have no solution, unique
solution and infinite solutions? Use Gaussian Elimination.
𝑥 − 𝑦 + 𝑧 = 1
𝑥 + 3𝑦 + 𝑎𝑧 = 2
2𝑥 + 𝑎𝑦 + 3𝑧 = 3
Answer by math_tutor2020(3816)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The given system

translates to the augmented matrix

The first three columns represent the x,y, and z coefficients in that order. The fourth column is the list of right hand side values.
The order from top to bottom is preserved. Meaning that the middle equation x+3y+az = 2 for instance, is represented by the middle row of numbers.
Let's use Gaussian Elimination to get this matrix into row echelon form (REF)
-----------------------------------------------
For each step below, I'll represent each matrix as a table. This way I can separate out each term more clearly with grid lines. However, your teacher likely won't want you to make such grid lines when making each matrix (it's unfortunate that matrices don't involve grid lines).
Here's the original matrix but in a tabular format
Let's subtract rows 1 and 2, which I'll denote as R1 and R2 respectively
The subtraction is R2 - R1 and it will replace the old R2. This notation is shown in blue to separate it from the matrix values.
The stuff in blue isn't part of the matrix, but I'm including it in the table anyway to clearly indicate which row is being altered.
| 1 | -1 | 1 | 1 | | | 0 | 4 | a-1 | 1 | R2 - R1 to R2 | | 2 | a | 3 | 3 | |
This step zeros out the first element of R2
Then we multiply everything in R2 by 1/4 = 0.25 to turn that 4 in R2 into a 1.
| 1 | -1 | 1 | 1 | | | 0 | 1 | 0.25(a-1) | 0.25 | 0.25*R2 to R2 | | 2 | a | 3 | 3 | |
Next, we'll need to zero out the first element of R3 as well. We'll compute R3 - 2*R1 to do this.
| 1 | -1 | 1 | 1 | | | 0 | 1 | 0.25(a-1) | 0.25 | | | 0 | a+2 | 1 | 1 | R3 - 2*R1 to R3 |
Notice at this point, nearly everything in the first column is 0 except for the first row with a 1 in it (which we call the pivot entry). The goal of row echelon form is to zero out items below the pivot.
The pivot of R2 is 1. We need to zero out everything below this. So we need to turn that a+2 into 0.
We do this by computing R3 - (a+2)*R2
| 1 | -1 | 1 | 1 | | | 0 | 1 | 0.25(a-1) | 0.25 | | | 0 | 0 | -0.25*(a^2+a-6) | -0.25(a-2) | R3 - (a+2)*R2 to R3 |
Now let's see what value of 'a' will make both items in R3 equal to 0
-0.25*(a^2+a-6) = 0
-0.25(a+3)(a-2) = 0
a = -3 or a = 2
and,
-0.25(a-2) = 0
a = 2
So if a = 2, then both items in R3 will be zeroed out. Having a row of all 0's indicates a dependent system with infinitely many solutions. Notice if a = 2, then adding the first two original equations yields the third equation exactly.
On the other hand, if a = -3, then the -0.25*(a^2+a-6) turns to zero while the other term -0.25(a-2) does not. We have an inconsistency. Therefore, we have an inconsistent system with no solutions when a = -3.
For any other case (ie when 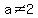 and when and when 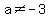 ), the system will have exactly one solution. ), the system will have exactly one solution.
That solution is (x,y,z) = ( 1, 1/(a+3), 1/(a+3) )
-----------------------------------------------
Answers:
Infinitely many solutions when a = 2.
No solutions when a = -3
Otherwise, there is exactly one solution.
|
|
|