SOLUTION: (a) Let f : (-\infty,0) \cup (0,\infty) \to \mathbb{R} be defined by f(x) = x - \frac{1}{x}.Show that f has no inverse function. (b) Let g : (0,\infty) \to \mathbb{R} be define

Algebra ->  College  -> Linear Algebra -> SOLUTION: (a) Let f : (-\infty,0) \cup (0,\infty) \to \mathbb{R} be defined by f(x) = x - \frac{1}{x}.Show that f has no inverse function. (b) Let g : (0,\infty) \to \mathbb{R} be define      Log On


   

Question 1189172: (a) Let f : (-\infty,0) \cup (0,\infty) \to \mathbb{R} be defined by
f(x) = x - \frac{1}{x}.Show that f has no inverse function.
(b) Let g : (0,\infty) \to \mathbb{R} be defined by
g(x) = x - \frac{1}{x}. Show that g has an inverse function.
How can you show this without graphing.
Thank you in advance
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Part (a)



Effectively, the domain is the set of nonzero numbers (aka anything but zero) and the range is the set of all real numbers

Let y = f(x)

We have the equation y+=+x+-+1%2Fx

We will swap the locations of x and y, then solve for y, to determine the inverse.

y+=+x+-+1%2Fx

x+=+y+-+1%2Fy

x+=+%28y%5E2%29%2Fy+-+1%2Fy

x+=+%28y%5E2+-+1%29%2Fy

xy+=+y%5E2+-+1

0+=+y%5E2-1+-+xy

y%5E2-xy-1+=+0

This equation is in the form ay%5E2%2Bby%2Bc+=+0 with a = 1, b = -x, c = -1

Apply the quadratic formula to solve for y

y+=+%28-b%2B-sqrt%28b%5E2-4ac%29%29%2F%282a%29

y+=+%28-%28-x%29%2B-sqrt%28%28-x%29%5E2-4%281%29%28-1%29%29%29%2F%282%281%29%29

y+=+%28x%2B-sqrt%28x%5E2%2B4%29%29%2F%282%29

y+=+%28x%2Bsqrt%28x%5E2%2B4%29%29%2F%282%29 or y+=+%28x-sqrt%28x%5E2%2B4%29%29%2F%282%29

We get two different results for y, which suggests we don't have a function overall.

Consider plugging in x = 1. This leads to...
y+=+%28x%2Bsqrt%28x%5E2%2B4%29%29%2F%282%29=+%281%2Bsqrt%281%5E2%2B4%29%29%2F%282%29=1.618 and y+=+%28x-sqrt%28x%5E2%2B4%29%29%2F%282%29=+%281-sqrt%281%5E2%2B4%29%29%2F%282%29+=+-0.618 (both are approximate)

In short, the input x = 1 leads to multiple outputs (roughly 1.618 and -0.618). This example shows that we don't have a function.

Therefore, the inverse of f%28x%29+=+x+-+1%2Fx does not exist when we're working with that specified domain. We'd need to make some kind of restriction in order to find the inverse.

=============================================================

Part (b)

Refer to the last bit of part (a) above. I mentioned we need to make a restriction on the domain for an inverse to be possible. Infinitely many such restrictions can be done to allow for f(x) to have an inverse. In this case, we're focusing on the positive real numbers 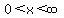0+%3C+x+%3C+infinity aka the interval effectively half of the original domain in part (a).

You'll follow the same exact steps as in the previous part. However, since x > 0, this means we only focus on y+=+%28x%2Bsqrt%28x%5E2%2B4%29%29%2F%282%29 which is indeed a function. Any x input in the domain leads to one and exactly one y output in the range.

We ignore y+=+%28x-sqrt%28x%5E2%2B4%29%29%2F%282%29 because every y value here is negative.

The fact that x > 0 in the domain of g(x) will lead to y > 0 in the range of the inverse of g.

Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.


            I will use the specific of the given function,  and will provide more simple solution. 


We are given the function  f(x) = x - 1%2Fx.


In part (a), the domain of this function is  (-oo,0) U (0,oo).


Notice that there is an identity  f(x) = f%28-1%2Fx%29,  valid for all x from the domain  (check it on your own).


It means that each image of f(x) has two pre-images: x and -1%2Fx.

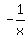One of these pre-images is positive number; the other pre-image is negative number.


So, the function f(x), defined on the whole domain, is not one-to-one function; 

THEREFORE, it has no an inverse function.




In part (b), the domain is restricted: now it is the set of all positive numbers.

On this set, the function f(x) = x - 1%2Fx is monotonically increasing  
(check it on your own, for example, taking the derivative).


Hence, it is one-to-one map.


Therefore, on the restricted domain, this function has an inverse function.

Solved.