SOLUTION: Let vector space M22 have the inner product defined as tr(U^T V ). Find the angle (measured in degrees) between the vectors A= | 2 6 | | 1 -3 | B= | 3 2 | | 1 0 |

Algebra ->  College  -> Linear Algebra -> SOLUTION: Let vector space M22 have the inner product defined as tr(U^T V ). Find the angle (measured in degrees) between the vectors A= | 2 6 | | 1 -3 | B= | 3 2 | | 1 0 |      Log On


   

Question 1167704: Let vector space M22 have the inner product defined as tr(U^T V ). Find the angle (measured in degrees) between the vectors
A=
| 2 6 |
| 1 -3 |
B=
| 3 2 |
| 1 0 |
Answer by ikleyn(52781) About Me  (Show Source):
You can put this solution on YOUR website!
.

The solution will be much easier if you represent the original matrices as the vectors, placing the second row after the first


    A = (2, 6, 1, -3),  B = (3, 2, 1, 0).


Now use the formula for the cosine of angle between the vectors in n-dimensional space R%5En


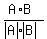    cos(A,B) = %28A%2AB%29%2F%28abs%28A%29%2Aabs%28B%29%29.



In your case, n= 4,  the scalar product (A*B) = 2*3 + 6*2 + 1*1 + (-3)*0 = 19,


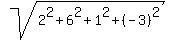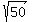the length of the vector  |A| = sqrt%282%5E2+%2B+6%5E2+%2B+1%5E2+%2B+%28-3%29%5E2%29 = sqrt%2850%29;


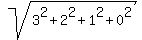the length of the vector  |B| = sqrt%283%5E2+%2B+2%5E2+%2B+1%5E2+%2B+0%5E2%29 = sqrt%2814%29;


    cos(A,B) = 19%2F%28sqrt%2850%29%2Asqrt%2814%29%29 = 0.718  (approximately).



Having the cosine, find the angle between the vectors as  arccos(0.718).


Use your calculator.

Solved and explained in all details.