SOLUTION: How does the rank of the following matrix depend on the value of t? (1,1,t) (1,t,1) (t,1,1)

Algebra ->  College  -> Linear Algebra -> SOLUTION: How does the rank of the following matrix depend on the value of t? (1,1,t) (1,t,1) (t,1,1)       Log On


   

Question 1167394: How does the rank of the following matrix depend on the value of t?
(1,1,t)
(1,t,1)
(t,1,1)
Answer by Resolver123(6) About Me  (Show Source):
You can put this solution on YOUR website!
We are given the following 3x3 matrix:

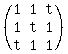
%28matrix%283%2C3%2C+1%2C1%2Ct%2C1%2Ct%2C1%2Ct%2C1%2C1%29%29

Compute the determinant det(A):
det%28matrix%283%2C3%2C+1%2C1%2Ct%2C1%2Ct%2C1%2Ct%2C1%2C1%29%29

det%28A%29+=+%28t+%2B+t+%2B+t%29+-+%28t%5E3%2B1%2B1%29=3t+-+t%5E3-2=-t%5E3+%2B+3t-2.
Let det%28A%29+=-t%5E3+%2B+3t-2=+0, or -%28t-1%29%5E2%28t%2B2%29+=+0.
Hence, det(A) = 0 if and only if t = 1 or t = -2.


Consider 3 cases:

Case 1: t ≠ 1 and t ≠ -2.
Then det(A) ≠  0, and so the matrix is of full rank, that is, rank(A) = 3.

Case 2: t = 1
Then the matrix is:
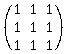
%28matrix%283%2C3%2C+1%2C1%2C1%2C1%2C1%2C1%2C1%2C1%2C1%29%29
All rows being identical means that there is only 1 linearly independent row. Hence, rank = 1.

Case 3: t = -2
Then we get the matrix:

%28matrix%283%2C3%2C+1%2C1%2C-2%2C1%2C-2%2C1%2C-2%2C1%2C1%29%29
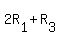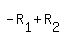Using the row operations 2R%5B1%5D+%2B+R%5B3%5D and -R%5B1%5D%2BR%5B2%5D, we get the row equivalent matrix
%28matrix%283%2C3%2C+1%2C1%2C-2%2C0%2C3%2C-3%2C0%2C-3%2C3%29%29
Using the row operation 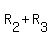R%5B2%5D%2BR%5B3%5D, we finally get
%28matrix%283%2C3%2C+1%2C1%2C-2%2C0%2C3%2C-3%2C0%2C0%2C0%29%29
This gives 2 linearly independent rows, and therefore, rank = 2.

Thus, the rank of the matrix depends on t as follows:
* Rank = 3 if t ≠ 1 and t ≠ -2.
* Rank = 2 if t = -2, and
* Rank = 1 if t = 1.