Question 1166880: Its several months before Christmas - New Year’s holiday season. Wholesalers for Barako’s Distilled Spirits have been busy taking orders and will soon be making deliveries to retailers to stock their shelves for the holiday season. During the next 2 weeks, Barako’s must decide on the quantities of its two principal products to be bottled and shipped.
The firm’s vice-president of sales, Sheilla Valdez, has negotiated contracts for minimum shipments to the firm’s customers. She has also created this year an attractive promotion campaign to attract new customers. Valdez expects that, as a result of the advertising program, the company’s sales during the holiday season will come close to those of the firm’s chief rival, Don John, whose aromatic cognac has been the top choice of discriminating holiday revelers for the past decade.
The following table indicates the minimum amounts that Valdez has contracted to supply the firm’s wholesalers. It also shows the maximum amounts that she believes the firm can sell this season - provided, of course, that the bottling plant has sufficient amounts of the necessary ingredients. This table also indicates the profit margins on the two products: a relatively low-price blend, New Rhythm and a premium product - Crown Alternate.
Product, Minimum Gallons, Maximum Gallons, Profit Margin(PhP/gallon)
New Rhythm, 30,000, 80,000, 2.50
Crown Alternate, 15,000, 40,000, 4.00
The two products are concoctions of Dr. M. dela Torre, research chemist at Barako’s, who is in charge of quality control. Besides a standard alcohol base, which is available in unlimited quantities, New Rhythm and Crown Alternate include a blend of two secret ingredients, which give the products their distinctive flavors and appeal. The amounts of these two ingredients (in percentage by volume) in the two products are as follows:
Product, % by volume of secret ingredient A, % by volume of secret ingredient B.
new Rhythm, 2.0, 3.0
crown alternative, 1.0, 5.0
The amount of the two ingredients that the company has available for blending during the production period are limited to 2,000 gallons of ingredient A and 2,500 gallons of ingredient X.
a. formulate lp models
b. Determine the product amounts that Barako’s should produce during the production period and the Barako’s profits. (Use Graphical Analysis)
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the graphical solution is shown below.
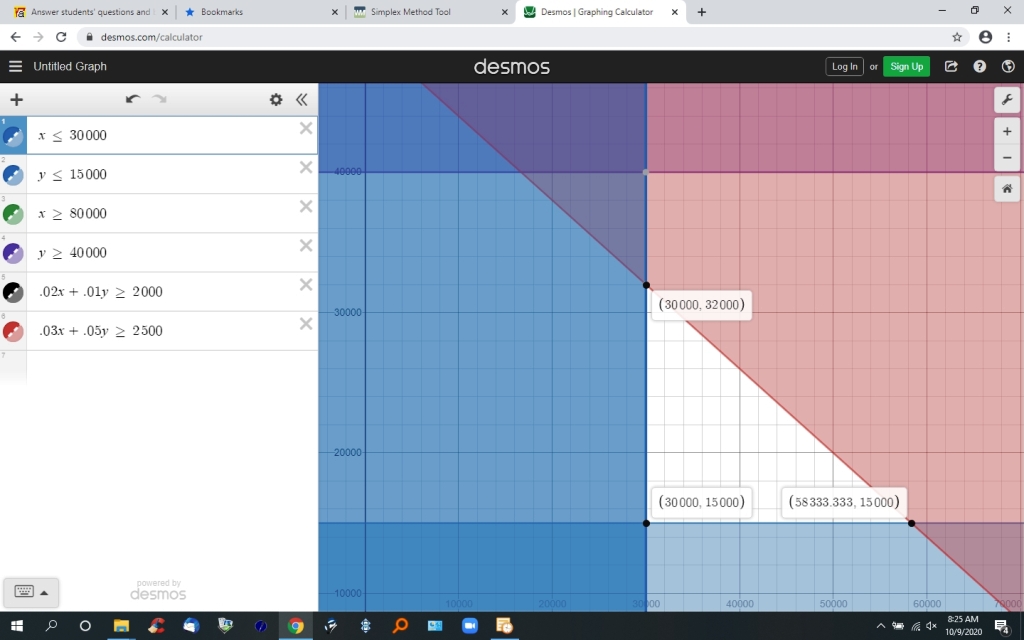
your variables are:
x = number of gallons of new rhythm.
y = number of gallons of crown alternate
your objective function is:
p = 2.5 * x + 4.0 * y
your constraints functions are:
x >= 30,000
y >= 15,000
x <= 80,000
y <= 40,000
.02 * x + .01 * y <= 2,000
.03 * x + .05 * y <= 2,500
using the desmos.com calculator, you would graph the OPPOSITE of these inequalities.
specifically, you would graph:
x <= 30,000
y <= 15,000
x >= 80,000
y >= 40,000
.02 * x + .01 * y >= 2,000
.03 * x + .05 * y >= 2,500
the feasible region on the graph is the area of the graph that is NOT shaded.
your max / min solution will be at the corner points of the feasible region.
you will evaluate your objective function at each of these corner points, using the value of x and the value of y shown in the format of (x,y) on the graph.
the following table shows the points and the value of the objective function as those points.
x y 2.5 * x + 4.0 * y
30,000 32,000 203,000
30,000 15,000 135,000
58,333.333 15,000 205,833.3325
the results show the maximum profit is attained when x = 58,333.333 and y = 15,000.
this means 58,333.333 gallons of new rhythm and 15,000 gallons of crown alternate are produced and sold.
all the constraints have to be satisfied as well.
when x = 58,333.333 and y = 15,000, .....
x >= 30,000 is satisfied.
y >= 15,000 is satisfied.
x <= 80,000 is satisfied.
y <= 40,000 is satisfied.
.02 * x + .01 * y = 1316.667 under 2000 is satisfied.
.03 * x + .05 * y = 2500 under 2500 is satisfied.
all the constraints are satisfied, therefore the maximum profit solution is confirmed to be good, based on the graphical analysis.
|
|
|