A square matrix is Invertible if and only if its determinant is non-zero.
 We find its determinant
We find its determinant


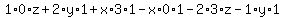

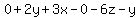

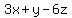 We can choose any values for x, y, z such that
We can choose any values for x, y, z such that
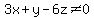 I'll arbitrary choose x=3, y=-2, z=1 (to make the determinant 1, so its
inverse will have all integer elements:
I'll arbitrary choose x=3, y=-2, z=1 (to make the determinant 1, so its
inverse will have all integer elements:
 Then its inverse is
Then its inverse is
 Edwin
Edwin