SOLUTION: Find the equation of the ellipse (𝑥+1)^2/4+(y−1)^2/1=1 reflected in the line 𝑦=−x+12 . Also sketch it.

Algebra ->  College  -> Linear Algebra -> SOLUTION: Find the equation of the ellipse (𝑥+1)^2/4+(y−1)^2/1=1 reflected in the line 𝑦=−x+12 . Also sketch it.      Log On


   

Question 1157498: Find the equation of the ellipse (𝑥+1)^2/4+(y−1)^2/1=1 reflected in the line 𝑦=−x+12 . Also sketch it.
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!

given:
the equation of the ellipse %28x%2B1%29%5E2%2F4%2B%28y-1%29%5E2%2F1=1+
reflected in the line y=-x%2B12
from %28x%2B1%29%5E2%2F4%2B%28y-1%29%5E2%2F1=1, we see that center of the ellipse is at
(-1,1)
since the center of the new ellipse reflected in the line will lie on the line which is perpendicular to given line, find the equation of the line perpendicular to given line and passes through (-1,1)

y=mx%2Bb
perpendicular line have a slope negative reciprocal to the slope of given line,
so m=-1%2F-1=1
y=1x%2Bb
use point (-1,1) to find b
1=1%28-1%29%2Bb
1=-1%2Bb
1%2B1=b
b=2
perpendicular line is y=x%2B2

now find intersection of these two lines
-x%2B12=x%2B2
-2%2B12=x%2Bx
2x=10
x=5
y=5%2B2=7
intersection is at
(5,7)

the point (5,7) is mid-point between the center to (-1,1) and the new center of the reflected ellipse (x,y) on the other side of the given line
so, (5,7)=(x%2F2,y%2F2)=> (x,y)=(10,14)
and, equation of the reflected ellipse is
%28x-10%29%5E2%2F4%2B%28y-14%29%5E2%2F1=1+
graph:



Answer by ikleyn(52776) About Me  (Show Source):
You can put this solution on YOUR website!
.

            The solution by @MathLover1 is  NOT  PRECISELY  CORRECT.

            Therefore,  I came to bring a  VALID  solution.

            The differences  (where @Mathlover1 made mistakes)  are shown in my post below. 



The given ellipse has the center at the point (-1,1).

Its major semi-axis is horizontal and have a length 2 = sqrt%284%29.

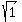Its minor semi-axis is verical and has a length of 1 = sqrt%281%29.


Now, when you reflect the given ellipse in the line y = -x+12, then, OBVIOUSLY,
the major semi-axis of the reflected ellipse will be VERTICAL of the length 2, and    <<<---=== Notice the difference with @MathLover1 (!)
the minor semi-axis of the reflected ellipse will be HORIZONTAL of the length 1.      <<<---=== Notice the difference with @MathLover1 (!)


Now let's find the coordinates of the CENTER of the reflected ellipse.

The given line is  y = -x + 12, or x + y = 12.

Hence, the perpendicular to this  line has, OBVIOUSLY, the form -x + y = c, where "c" is a constant.

We will find the constant "c", using the condition that the center of the given ellipse (-1,1) lies at the perpendicular line.

-(-1) + 1 = 2 gives the value of "c" as 2;  therefore, the equation of the perpendicular line is -x + y = 2,  or  y = x+2.

The given line  y = -x+12 intersect the "mirror" line y = x+2 at the point x= 5, y= 7.


The point (5,7) is mid-point between the center to (-1,1) and the new center of the reflected ellipse (x,y) on the other side of the given line.

So, the center of the reflected ellipse is the point (11,13).   <<<---=== Notice the difference with @MathLover1 (!)


Thus the equation for the reflected ellipse is

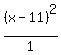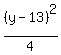    %28x-11%29%5E2%2F1 + %28y-13%29%5E2%2F4 = 1.               <<<---=== Notice the difference with @MathLover1


And, finally, the plot

Solved.