Question 1136613: At the end of spring break, Lucy left the beach and drove back towards home, driving at a rate of 50 mph. Lucy's friend left the beach for home 30 minutes (half an hour) later, and drove 55 mph. How long, in hours, did it take Lucy's friend to catch up to Lucy?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39670)   (Show Source): (Show Source):
Answer by ikleyn(53318)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
When the friend left the beach, Lucy was (0.5 hours) * 50 mph = 25 mph ahead.
But the friend moves faster, decreasing the distance between them by 5 = 55 - 50 miles per hour.
So, the friend will catch Lucy in 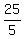 = 5 hours. = 5 hours.
Algebra solution
Algebra solution is this equation
50*(t+0.5) = 55*t,
saying that both of them cover the same distance from the start to the catching point.
In this equation " t " is the time starting from the moment, when the friend began his move.
Simplify and solve it
50t + 25 = 55t
25 = 55t - 50t
25 = 5t
t = 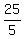 = 5 hours.
The same answer as in the very first solution. = 5 hours.
The same answer as in the very first solution.
Solved.
--------------------
See introductory lessons on Travel and Distance problems
- Travel and Distance problems
- Travel and Distance problems for two bodies moving in opposite directions
- Travel and Distance problems for two bodies moving in the same direction (catching up)
in this site.
They are written specially for you.
You will find the solutions of many similar problems there.
Read them and learn once and for all from these lessons on how to solve simple Travel and Distance problems.
Become an expert in this area.
/\/\/\/\/\/\/\/\/\/\/
Ignore the post by @josgarithmetic, since it is totally nonsensical.
|
|
|