Question 1134409: Find four numbers in G.P whose sum is 85 and product is 4096.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The four numbers are
a, ar, ar^2, ar^3
Their sum is 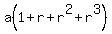 ; their product is ; their product is 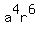 . So . So
 and and 
Since both the sum and product are whole numbers, the four numbers are almost certainly whole numbers. So solve the problem by logical trial and error.
One way is to start with the given product and find the numbers with that product whose sum is 85.

A bit of playing around with that finds a=1 and r=2^2=4 is a solution; that gives the four numbers as 1, 4, 16, and 64; and their sum is 85.
Or another way would be to start with the sum of 85 and find four numbers with that sum whose product is 4096. This one takes a bit more problem solving skill....



Again a=1 and r=4 satisfies this equation, because 1+r = 5 and 1+r^2 = 17.
And here is another way to start with the sum of 85 and find the solution by logical reasoning; this path is probably easier to see than the one described above.

Since the numbers are probably whole numbers, this means a has to be either 1 or 5. And a bit of playing with those possibilities quickly shows it can't be 5. So a = 1, and it takes only a bit more trial and error to find that r=4. Then verifying the solution by showing that the product is 4096 completes the problem.
|
|
|