Question 1122472: Consider the following points.
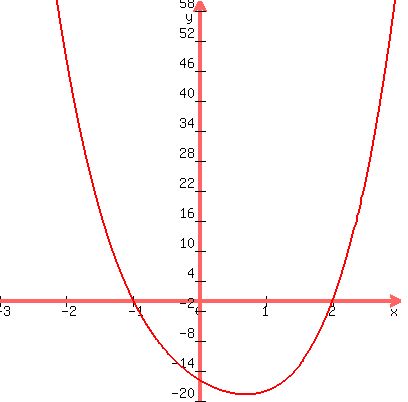
(−2, 48), (−1, 0), (0, −16), (1, −18), (2, 0)
(a) Determine the polynomial function of least degree whose graph passes through the given points.
Answer by greenestamps(13216)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given n points, a polynomial of degree (n-1) or less can fit the points. With 5 points as in this problem, the polynomial that produces the 5 points will have degree 4 or less.
We can use the method of finite differences to see if the polynomial might have degree less than 4.
48 0 -16 -18 0
-48 -16 -2 18
32 14 20
-18 6
24
We don't get a row of constant differences before the 4th row of differences, so the polynomial that produces the given points will be degree 4.
The "24" in the 4th row of differences also tells us that the leading coefficient of the polynomial will be 24/(4!) = 24/24 = 1.
The general polynomial of degree 4 is
y = ax^4+bx^3+cx^2+dx+e
Form a system of 5 equations in the 5 variables using the x and y value of the given points. It will turn out that there are some shortcuts that make this particular system of equations relatively easy to solve.
(1) x=-2: 16a - 8b + 4c - 2d + e = 48
(2) x = -1: a - b + c - d + e = 0
(3) x = 0: e = -16
(4) x = 1: a + b + c + d + e = -18
(5) x = 2: 16a + 8b + 4c + 2d + e = 0
Adding equations (2) and (4) gives us



(6) 
Adding equations (1) and (5) gives us



(7) 
Then solving equations (6) and (7) gives us a=1 (which we already knew) and c=6.
Subtracting equation (2) from equation (4) gives us

(8) 
Subtracting equation (1) from equation (5) gives us

(9) 
Then solving equations (8) and (9) gives us b = -1 and d = -8.
So we have our coefficients:
a = 1; b = -1; c = 6; d = -8; e = -16
The polynomial of least degree that passes through the 5 given points is

A graph that passes through (-2,48), (-1,0), (0,-16), (1,-18) and (2,0)...
|
|
|