SOLUTION: pls help me to answer: if the sum of the reciprocals of the roots of the equation 3x^2 + 7x + k is -7/3, what is k?

Let "a and "b" be the roots.

We are given that   = .

Write the left side with the common denominator, which is the product ab. You will get

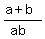 = .        (1)


Now notice that by the Vieta's theorem (!)  a + b = .    (2)


    Vietas's theorem, part 1:  the sum of the roots of a quadratic equation is equal to the coefficient at "x" with the opposite sign, 
    divided by the coefficient at x^2.


Great !!  Now substitute (2) into equation (1) to get

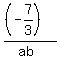 = .    (3)


It implies that   = 1,     or     ab = 1.    (4)


Now notice that by Vieta's theorem (its second part)  ab = 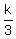.       (5)


    Vietas's theorem, part 2:  the product of the roots of a quadratic equation is equal to the constant term of the equation, 
    divided by the coefficient at x^2.


Now from (4) and (5) you have  ab = 1 = ,

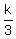which implies  k = 3.


The problem is SOLVED, and the answer is:  k = 3.