Question 1092551: please help me to answer: the sum of lengths of all edges of a rectangular box is 140 dm and the distance from one corner of the box from the farthest corner
is 21 cm. What is the total surface area of the box?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
please help me to answer: the sum of lengths of all edges of a rectangular box is 140 dm and the distance from one corner
of the box  to the farthest corner is 21 cm. What is the total surface area of the box? to the farthest corner is 21 cm. What is the total surface area of the box?
~~~~~~~~~~~~~~~~~
It is a nice problem, and it has beautiful and unexpected solution.
I will show you the solution right now, but first I need to fix one obvious ERROR in your condition: replace 140 dm by 140 cm.
So, all dimensions are in centimeters.
Let x, y and z be three perpendicular dimensions of the box: the length, the width and the height respectively.
Then you are given
4x + 4y + 4z = 140 cm (the sum of lengths of all 12 edges), or, dividing by 4 both sides,
x + y + z = 35 cm. (1)
Also, you are given that
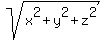 = 21 cm. (2) ("the distance from one corner of the box to the farthest corner is 21 cm.")
I will not go to explanation why (2) is that distance: it is easy consequence of the Pythagorean theorem in 3D.
Now square both sides of (2) to get = 21 cm. (2) ("the distance from one corner of the box to the farthest corner is 21 cm.")
I will not go to explanation why (2) is that distance: it is easy consequence of the Pythagorean theorem in 3D.
Now square both sides of (2) to get
 = 21^2 = 441. (3)
Thus we have these two equations simultaneously:
x + y + z = 35, (1) = 21^2 = 441. (3)
Thus we have these two equations simultaneously:
x + y + z = 35, (1)
 = 441. (3)
Square both sides of equation (1). You will get = 441. (3)
Square both sides of equation (1). You will get
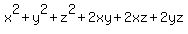 = =  = 1225.
In the last equation, replace = 1225.
In the last equation, replace 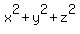 by 441, based on (3). You will get
441 + 2xy + 2xz + 2 yz = 1225, ====>
2xy + 2xz + 2 yz = 1225 - 441, ====>
2*xy + 2*xz + 2*yz = 784.
Now notice that the left part of the last equation is nothing else as the total surface are of the box.
So, we got this
Answer. The total surface area of the box is equal to 784 cm^2. by 441, based on (3). You will get
441 + 2xy + 2xz + 2 yz = 1225, ====>
2xy + 2xz + 2 yz = 1225 - 441, ====>
2*xy + 2*xz + 2*yz = 784.
Now notice that the left part of the last equation is nothing else as the total surface are of the box.
So, we got this
Answer. The total surface area of the box is equal to 784 cm^2.
*** Solved ***
|
|
|