SOLUTION: Jennifer wants to make 10 gal. of a 40% alcohol solution by mixing together a 10% alcohol solution and a 60% alcohol solution. How much of each solution must she us? This is so c

Algebra ->  College  -> Linear Algebra -> SOLUTION: Jennifer wants to make 10 gal. of a 40% alcohol solution by mixing together a 10% alcohol solution and a 60% alcohol solution. How much of each solution must she us? This is so c      Log On


   

Question 1090336: Jennifer wants to make 10 gal. of a 40% alcohol solution by mixing together a 10% alcohol solution and a 60% alcohol solution. How much of each solution must she us? This is so confusing please help me out!
Found 2 solutions by KMST, josgarithmetic:
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
In math class, "mixture problems" are solved as a set of linear equations.
Defining variables:
x= volume of 10% alcohol solution to be used, in gallons
y= volume of 60% alcohol solution to be used, in gallons
Setting up equations:
Because Jennifer wants to make 10 gallons of solution,
x%2By=10 .
Because the final solution must contain 40% alcohol,
the alcohol amounts in the mixed solutions, must add to the alcohol amount in the final solution.
The equation stating that is
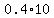0.1x%2B0.6y=0.4%2A10 .
0.4%2A10 represents the amount of alcohol in 10 gallons of 40% solution,
0.1x represents the amount of alcohol in x gallons of 10% solution, and
0.6y represents the amount of alcohol in y gallons of 60% solution.
Those amounts are expressed in the same units, so it does not matter what those units are.
Solving the system of equations:
0.1x%2B0.6y=0.4%2A10 would be simplified to 0.1x%2B0.6y=4 ,
and every term would be multiplies times 10 to get the equivalent equation
x%2B6y=40
Then you would solve the system
system%28x%2By=10%2Cx%2B6y=40%29
by whichever way is easier for you.
Maybe you would choose substitution,
solving x%2By=10 for x to find x=10-y ,
and then substituting the expression 10-y for x
in x%2B6y=40 to find y first.
10-y%2B6y=40
10%2B5y=40
5y=40-10
5y=30
y=30%2F5
highlight%28y=6%29 .
After that, it would be easiest to substitute the value found
for y in equation x=10-y , to find
x=10-6
highlight%28x=4%29 .

NOTE:
In pharmaceutics class, or in chemical engineering class,
you would ask what was meant by alcohol.
Is it ethanol (ethyl alcohol) or isopropyl alcohol?
You would ask for clarification about the units, and figure out units for the amount of alcohol.
You would know that when you mix volumes of solutions, the final volume is not exactly the sum of the volumes, but the sum may work as a good approximation for your purposes.

Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
                 VOLUME       ALCOHOL

40% Alcohol       x           0.6x

10% Alcohol      10-x         0.10(10-x)

MIXTURE          10           0.6x+0.10(10-x)

%280.6x%2B0.1%2810-x%29%29%2F10=0.4
0.6x%2B1-0.1x=0.4%2A10
6x%2B10-x=40
5x=30
highlight%28x=6%29-----gallons of the 60%
highlight%284%29-------gallons of the 10%