.
I am having trouble figuring out how to solve this problem.
Find all real solutions to the equation 40-106e^x+101e^2x-41e^3x+6e^4x=0.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let us introduce new variable z =  , Then the equation will take a form
p(z) = 6z^4 - 41z^3 +101z^2 - 106z + 40 = 0.
One root is z=1. You can check it making direct calculation.
So, the polynomial has the divisor (z-1).
The quotient
, Then the equation will take a form
p(z) = 6z^4 - 41z^3 +101z^2 - 106z + 40 = 0.
One root is z=1. You can check it making direct calculation.
So, the polynomial has the divisor (z-1).
The quotient 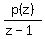 is q(z) =
is q(z) = 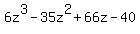 (long division).
The root of the cubic polynomial is z=2. You can check it making direct calculation.
So, the polynomial has the divisor (z-2).
The quotient
(long division).
The root of the cubic polynomial is z=2. You can check it making direct calculation.
So, the polynomial has the divisor (z-2).
The quotient 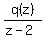 is r(z) =
is r(z) = 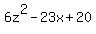 (long division).
r(z) has the roots 2.5 and
(long division).
r(z) has the roots 2.5 and  (quadratic formula).
So, the polynomial p(z) has the roots 1, 2, 2.5 and
(quadratic formula).
So, the polynomial p(z) has the roots 1, 2, 2.5 and  .
Since z =
.
Since z = 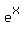 , the original polynomial has the roots
x = ln(1) = 0, x = ln(2), x = ln(2.5) and x = ln((3/4)).
, the original polynomial has the roots
x = ln(1) = 0, x = ln(2), x = ln(2.5) and x = ln((3/4)).
Solved.