Question 1054139: please help me to solve this problem.
During a certain week, a small wind generator and a small hydro unit together produce 5880 kWh, with the wind generator operating only 85.0% of the time. During another week, the two units produce 6240 kWh, with the wind generator working 95.0% of the time and the hydro unit down 7.50 h for repairs. Assuming that each unit has a constant output when operating, find the number of kilowatts produced by each in 1.00 h.
Do not round intermediate results. Round only final answers. Round to the nearest integer.
wind generator:
hydro unit:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! assuming that these operate 24 hours a day and that there are 7 days in a week, then the total number of hours each is up, if they are up 100% of the time, will be 7 * 24 = 168 hours.
based on that assumption.
85% of the time will be .85 * 168 = 142.8 hours.
95% of the time will be .95 * 168 = 159.6 hours.
the general formula is rate * time = quantity of work produced.
the quantity of work produces is in kilowatt hours.
the time is in hours.
the rate will be in kilowatt hours per hour.
let w = the rate of the wind generator.
let h = the rate of the hydro unit.
for the first week, you get:
142.8 * w + 168 * h = 5880
for the second week, you get:
159.6 * w + (168 - 7.5) * h = 6240.
this can be simplified to 159.6 * w + 160.5 * h = 6240
you have 2 equations that need to be solved simultaneously.
they are:
142.8 * w + 168 * h = 5880
159.6 * w + 160.5 * h = 6240
assuming that you know how to solve equations simultaneously, i'll jump to the answer to tell you that the simultaneous solution to these equation is:
w = 26.86084142 kilowatts per hour.
h = 12.16828479 kilowatts per hour.
your solution is that the wind generator generates 27 kilowatts per hour and the hydro unit generates 12 kilowatts per hour.
i also solved this graphically as shown below.
look for the intersection between the lines of the two equations.
the coordinate point of the intersection confirms the solution.
in the graph, x represents w and y represents h.
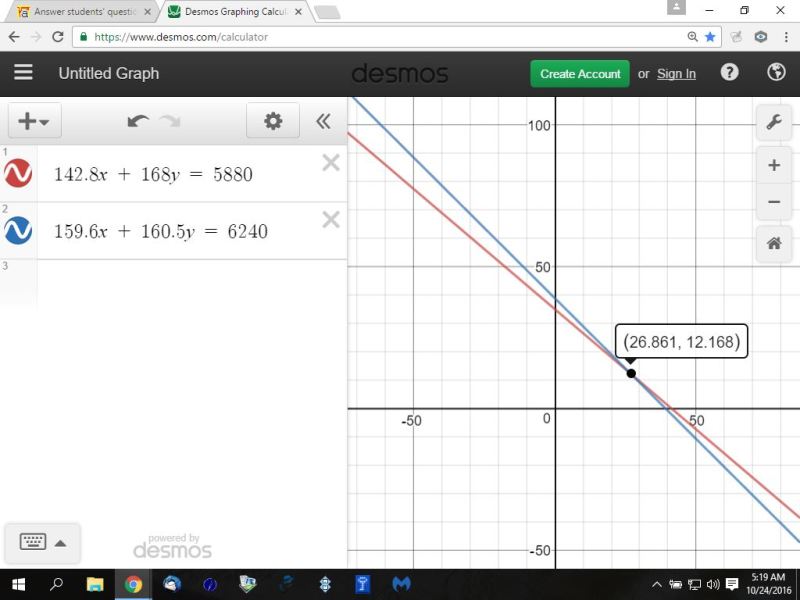
you can confirm the solution is correct, by replacing w with 26.86084142 and h with 12.16828479 in the following equations.
142.8 * w + 168 * h = 5880
159.6 * w + 160.5 * h = 6240
if my assumptions about the number of hours in a week being equal to 168, then i believe this solution is correct.
check it out and see if you think that this is reasonable.
|
|
|