Question 1045619: Analyze the linear transformation L(x) = Dx that transforms the vector x = [1 4
] to the
vector L(x) = [3 6
] and also transforms the vector x = [2 5
] to the vector L(x) = [0 9
] by
doing the following:
1. Find the entries of the 2x2 matrix D that result in this transformation. 2. Describe, referencing the linear transformation, how the entries of matrix D were determined. 3. Describe the relationship between the determinant of matrix D, the area of S, and the area of the transformed figure P by considering a 2x2 square S in the xy-plane.
Note: The linear transformation L(x) transforms the square S into another shape P in the xy-plane.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! First of all, the format of your notation is a little awkward.
If you're operating with row vectors then the linear transformation should be
L(x) = xD, and not L(x) = Dx (which is used when x is a column vector.)
1.  . .
2. The entries of D were determined by first letting  , and then making the following substitutions: , and then making the following substitutions:
L(< 1,4 >) = < 1,4 >*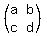 = < 3,6 >, and = < 3,6 >, and
L(< 2,5 >) = < 2,5 >*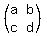 = < 0,9 >. = < 0,9 >.
The first equation gives the system a + 4c = 3 and b + 4d = 6.
The second equation gives the system 2a + 5c = 0 and 2b + 5d = 9.
Solving for a, b, c, and d simultaneously, we get a = -5, b = 2, c = 2, and d = 1.
3. Let S be the square with vertices (0,0), (0,2), (2,2), and (2,0).
S is sufficiently represented by the vectors < 0,2 > and < 2,0 > so it's enough to consider the effect of L on these two vectors.
L(< 0,2 >) = < 0,2 >*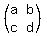 = < 4,2 >, and = < 4,2 >, and
L(< 2,0 >) = < 2,0 >*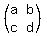 = < -10,4 >. = < -10,4 >.
Hence the linear transformation L transforms the square S into a parallelogram P three of whose vertices are (-10,4), (0,0),
and (4,2), and with an area of
 . .
Now S has area 2*2 = 4, and since  , we get , we get
36 = Area of P = |D|*(Area of S) = 9*4.
|
|
|