Question 1044529: use linear programming to maximize z=10x+15y subject to
x+4y < 360
2x+y<300
x>0, y>0
all signs are equal to
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The constraints are
 . That is the quadrilateral limited by the lines . That is the quadrilateral limited by the lines  : :  . .
Sketching a graph is very helpful.
It allows you to "see" the feasible region you are working with.
In this case, it is the region below both blue an green lines,
above the x-axis, and
to the right of the y-axis.
The feasible region is obviously the quadrilateral 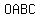 . .
It is easy to see that shrewdly selected test point 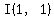 , ,
within 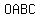 , meets the requirement of all the constraints, , meets the requirement of all the constraints,
and if you move away from that point crossing over any boundary line,
you cease to meet all requirements.
The line  is the y-axis. is the y-axis.
The line  is the x-axis. is the x-axis.
Those two lines intersect at  , the origin. , the origin.
To graph  , I connected with a straight line its x- and y-intercept. , I connected with a straight line its x- and y-intercept.
I found those intercepts by solving
 ---> ---> ---> ---> to get point to get point 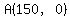 , ,
and
 ---> ---> to get point to get point 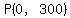 . .
To graph  , I did the same. , I did the same.
I found its x- and y-intercepts by
solving
 ---> --->
 ---> ---> to get point to get point  , ,
and
 ---> --->
 ---> ---> to get point to get point 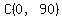 . .
I also had to find the point where  and and  intersect. intersect.
I did it by solving
 to get point to get point 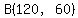 . .
There are many ways to salve that. Here is one:
 --> --> --> --> --> --> --> --> --> --> --> --> --> --> --> --> --> --> --> -->
Finally, we need to maximize  , a function of , a function of  and and  , within that feasible region. , within that feasible region.
Because the boundaries and the function are linear,
the maximum will be
either at one of the vertices of the feasible region,
or all along one of the edges of that region.
It could have been obvious to us from the start that the maximum would be at point 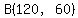 (see note below), (see note below),
but the recipe usually taught to solve this kind of problems involves calculating the value of the function  at every vertex. at every vertex.
The idea may be the educational value of
encouraging practice,
valuing hard work, and
helping you visualize the situation.
So, we worked hard to get to this point, and we continue along the expected path.
At  : :
 , obviously no maximum. , obviously no maximum.
At 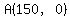 : :

At 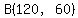 : :

At 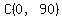 : :
 . .
The maximum is  at point at point  . .
NOTE:
Versions of this type of problem are very popular.
You have  , telling you the feasible region is in quadrant I. , telling you the feasible region is in quadrant I.
There are two boundary line constraints:  , ,
with all positive coefficients,
telling you that the feasible region is below two lines with positive x- and y-intercepts.
and the function to maximize,  , has positive coefficients. , has positive coefficients.
To make you work harder, hey make the maximum be at the intersection of the two lines,
by making the slope of the lines  , ,  , ,
be in between the slopes,  and and 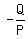 , of the two slanted boundary lines. , of the two slanted boundary lines.
So, in this case, we could immediately see that
the boundary line slopes are  and and  , ,
with the slope of any  line, line,
 , in between them , in between them  . .
That tells us that the maximum is at the intersection of the two slanted boundary lines,
 ---> point ---> point 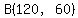 . .
So the maximum is  . .
|
|
|