.
determine the value of a so that the system
x + y - z = 1
2x + 3y + az = 3
x + ay + 3z = 2
has
1)infinitely many solution
2)no solution
3)unique solution
~~~~~~~~~~~~~~~~~~~~~~~~~
x + y - z = 1, (1)
2x + 3y + az = 3, (2)
x + ay + 3z = 2. (3)
One way is to calculate the determinant of the matrix on the left and equalize it to zero.
But calculating the determinant of the 3x3 matrix was, probably, not what you were dreamed on.
So, it is better to reduce the given 3x3 system to a 2x2 system first.
How we will do it? But of course, by eliminating "x".
So, multiply the equation (1) by 2 (both sides) and then distract it from the equation (2). You will get
(3y-2y) + (az-(-2z)) = 3-2, or
y + (a+2)z = 1. (4)
Next, distract the equation (1) from the equation (3) (both sides). You will get
(ay-y) + (3z - (-z)) = 2-1, or
(a-1)y + 4z = 1. (5)
Let us write the equations (4) and (5) as a system, one under another.
y + (a+2)z = 1. (4')
(a-1)y + 4z = 1. (5')
This system is equivalent to (1)-(3) in the obvious sense.
Now the determinant of the matrix on the left is
det(A) = 4 - (a+2)*(a-1) =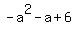 
The theory says: the system (4'), (5') has a unique solution
if and only if the determinant det(A) is not zero.
It has no solution OR infinitely many solution
if and and only if the determinant det(A) is zero.
So, let us find the singular values of "a" that are the roots of this quadratic equation:
= 
.
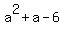Factor the left side, and you will get
(a+3)*(a-2) = 0
with the roots a = -3 and a = 2.
At a = -3 the equations (4'), (5') become
y - z = 1. (6)
-4y + 4z = 1. (7)
and evidently have no common solution.
At a = 2 the equations (4'), (5') become
y + 4z = 1. (8)
y + 4z = 1. (9)
and evidently have infinitely many solutions.
Answer. At a = 2 the original system has infinitely many solutions.
At a = -3 the original system has no solutions.
At all other values of "a" the original system has a unique solution.
Solved.
