Question 1042309: given the homogenous system x+2y-z=0,3x-3y+2z=0,-x-11y+kz=0 . a)find the value of k for the system has a non trival solution .b)solve for the value of k
Answer by ikleyn(52914)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
given the homogeneous system x+2y-z=0,3x-3y+2z=0,-x-11y+kz=0.
a) find the value of k for the system has a non trival solution .
b) solve for the value of k
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
x + 2y - z = 0, (1)
3x - 3y + 2z = 0, (2)
-x - 11y + kz = 0. (3)
I know two ways to solve it.
One way is to calculate the determinant of the 3x3 matrix on the left and to equalize it to zero, and then find
the value of "k" from this condition.
This way is quite boring and is not so much educational.
So I choose another way.
Let us multiply the equation (1) by 4 (both sides) and write the modified equation (1) along with the equation (2). You will have
4x + 8y - 4z = 0, (1')
3x - 3y + 2z = 0. (2')
Now distract equation (1') from (2'). You will get
-x - 11y + 6z = 0. (4)
Now I will write the equation (3) right under the equation (4).
-x - 11y + kz = 0. (3')
Now compare (3') and (4), and you momentarily see that the equations (4) and (3') are identical at k = 6, and are different at any other value of k.
In other words, at k = 6 the system (1), (2) and (3) has linearly dependent equations.
It means that at k = 6 the system is degenerated (singular) and has non-trivial solution.
And we can easily find it by taking, for example, z = 1 (actually, any arbitrary value) and then find x and y from (1) and (2)
x + 2y - 1 = 0, (1'') ( I substituted z=1 into (1) and (2) ! )
3x - 3y + 2 = 0. (2'')
It is the same as
x + 2y = 1, (5)
3x - 3y = -2. (6)
Now express x = 1-2y from (5) and substitute it into (6). You will get
3(1-2y) - 3y = -2 ---> 3 - 6y - 3y = -2 ---> -9y = -5 ---> y = 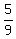 .
Then x = 1-2y = 1 - .
Then x = 1-2y = 1 - 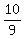 = = 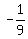 .
Thus, a non-trivial solution at k = 6 is x = .
Thus, a non-trivial solution at k = 6 is x = 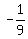 , y = , y = 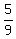 and z = 1.
Or, if you love integer numbers more than rational, take
x = -1, y = 5 and z = 9.
Answer. The singular value for k is 6 and the non-trivial solution in this case is (x,y,z) = (-1, 5, 9). and z = 1.
Or, if you love integer numbers more than rational, take
x = -1, y = 5 and z = 9.
Answer. The singular value for k is 6 and the non-trivial solution in this case is (x,y,z) = (-1, 5, 9).
|
|
|