Question 1042222: or which value of k does the following system of equation have non trivial solution (k-3)x+y=0,x+(k-3)y=0
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20067)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This problem is very badly worded. My question here is:
What is meant by a "non-trivial" solution????
 No matter what value k has, (0,0) will be a solution,
because regardless of k, if we substitute x=0, y=0,
we get:
No matter what value k has, (0,0) will be a solution,
because regardless of k, if we substitute x=0, y=0,
we get:
 which is equivalent to
which is equivalent to
 And since they are linear equations, they MUST
have (0,0) as a solution. So (0,0) is not to
be considered as a "trivial" solution. Otherwise
the answer would be "there are no values of k
that would not cause the system to have the solution
(0,0).
So I suppose what is meant by a "non-trivial"
solution is that they have only one solution and
not an infinite number of solutions. It is bad
wording to use "having a non-trivial solution" to
mean "having only one solution", or "independent
and consistent". You might point this out to your
teacher.
If k=3, then we have:
And since they are linear equations, they MUST
have (0,0) as a solution. So (0,0) is not to
be considered as a "trivial" solution. Otherwise
the answer would be "there are no values of k
that would not cause the system to have the solution
(0,0).
So I suppose what is meant by a "non-trivial"
solution is that they have only one solution and
not an infinite number of solutions. It is bad
wording to use "having a non-trivial solution" to
mean "having only one solution", or "independent
and consistent". You might point this out to your
teacher.
If k=3, then we have:


 which is the x-axis and the y-axis which
is a non-trivial independent system with
one solution, x=0, y=0. So k=3 is a value
of k for which the system does not have a
trivial solution.
If k ≠ 3, then k-3 ≠ 0 and so
we can divide by it.
So if k ≠ 3, we can solve them both
for y
which is the x-axis and the y-axis which
is a non-trivial independent system with
one solution, x=0, y=0. So k=3 is a value
of k for which the system does not have a
trivial solution.
If k ≠ 3, then k-3 ≠ 0 and so
we can divide by it.
So if k ≠ 3, we can solve them both
for y


 Their slopes are
Their slopes are 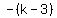 and and 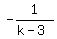 If the slopes are equal, the system will be
dependent, and their graphs will be the same
line, and there will be an infinite number of
solutions.
For them to have an infinite number of solutions,
then their equations and, in this case, also their
slopes will be the same:
If the slopes are equal, the system will be
dependent, and their graphs will be the same
line, and there will be an infinite number of
solutions.
For them to have an infinite number of solutions,
then their equations and, in this case, also their
slopes will be the same:
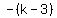  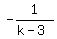 and k ≠ 3.
Multiply both sides by -1 and k ≠ 3.
Multiply both sides by -1
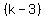  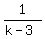 and k ≠ 3.
Multiply both sides by (k-3) and k ≠ 3.
Multiply both sides by (k-3)
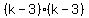   FOIL:
FOIL:
   Get 0 on the right by subtracting 1 from both sides:
Get 0 on the right by subtracting 1 from both sides:
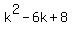   Factor the left side
Factor the left side
   k-4 = 0, k-2 = 0
k = 4, k = 2
So the system will have infinitely many solutions,
and be a dependent system if and only if k ≠ 4 and
k ≠ 2.
So if and only if k ≠ 4 and k ≠ 2, the two lines
will intersect at the origin and will not be the
same line and the system will be independent and
consistent and there will be only 1 solution.
But please point out to your teacher about the
bad wording of this problem. A dependent system
has infinitely solutions and cannot be said to
"have a non-trivial solution".
Edwin
k-4 = 0, k-2 = 0
k = 4, k = 2
So the system will have infinitely many solutions,
and be a dependent system if and only if k ≠ 4 and
k ≠ 2.
So if and only if k ≠ 4 and k ≠ 2, the two lines
will intersect at the origin and will not be the
same line and the system will be independent and
consistent and there will be only 1 solution.
But please point out to your teacher about the
bad wording of this problem. A dependent system
has infinitely solutions and cannot be said to
"have a non-trivial solution".
Edwin
Answer by ikleyn(52943)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
 At which value of k does the following system of equation have non trivial solution (k-3)x+y=0,x+(k-3)y=0 ? At which value of k does the following system of equation have non trivial solution (k-3)x+y=0,x+(k-3)y=0 ?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This wording is very usual, standard and typical for systems of linear equations.
The "trivial solution", by the definition, is zero solution (x,y) = (0,0).
When they are asking about a non-trivial solution, they actually ask:
"at which value of "k" the system is degenerated ?"
In other words,
"at which value of "k" the system has more than one solution ?"
( provided that it always has a zero solution (0,0). )
It depends and it is defined entirely by the value of the determinant of the matrix of this system.
If the determinant is non-zero, the system has only trivial zero solution.
If the determinant is zero, then there are "non-trivial" solutions.
The matrix in this case is 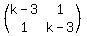 , and its determinant is , and its determinant is 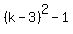 .
The condition of zeroing the determinant is .
The condition of zeroing the determinant is
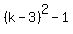 = =  , or , or 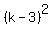 = =  , or k-3 = +/- , or k-3 = +/-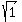 , or k-3 = +/-1,
which implies k = 4 or k = 2.
At k = 4 the system becomes
x + y = 0,
x + y = 0.
Clearly, it is dependent; represents one straight line; and has infinitely many solutions.
At k = 2 the system becomes
-x + y = 0,
x - y = 0.
Again, it is dependent; represents one straight line; and has infinitely many solutions. , or k-3 = +/-1,
which implies k = 4 or k = 2.
At k = 4 the system becomes
x + y = 0,
x + y = 0.
Clearly, it is dependent; represents one straight line; and has infinitely many solutions.
At k = 2 the system becomes
-x + y = 0,
x - y = 0.
Again, it is dependent; represents one straight line; and has infinitely many solutions.
|
|
|