Question 1017899: Find the values of a and b that will make the function continuous every where. Justify.
f(x)=
x^2+11x+10/x+1, x<-1
e^2ax , -1<= x <= 1
bx^2-ax, x>1
thank you in advance!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe what you meant is
  
The pieces of that function are continuous in
   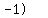 , , 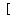   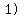 , and , and 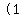    . .
We just have to make it continuous at  and and  . .
For  , we have , we have  . .
For  , ,  , and , and
 , ,
so for  to be continuous at to be continuous at  , ,
it must be  --> --> --> --> --> -->
For  , we have , we have  . .
For 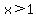 , ,  , and , and
 , ,
so for  to be continuous at to be continuous at  , ,
it must be  . .
Since we knew that
 --> --> , ,
substituting into  , we get , we get  --> -->
|
|
|