SOLUTION: If {{{f(x) = (x^2 - a^2)/(x - a)}}} , when I find the value when {{{x=a}}}, its {{{0/0}}} which is, well you know. But when I further simplify the function, I get {{{f(x) = x +

Algebra ->  College  -> Linear Algebra -> SOLUTION: If {{{f(x) = (x^2 - a^2)/(x - a)}}} , when I find the value when {{{x=a}}}, its {{{0/0}}} which is, well you know. But when I further simplify the function, I get {{{f(x) = x +       Log On


   

Question 1001468: If f%28x%29+=+%28x%5E2+-+a%5E2%29%2F%28x+-+a%29 , when I find the value when x=a, its 0%2F0 which is, well you know.
But when I further simplify the function, I get f%28x%29+=+x+%2B+a , which has a value for x+=+a, which is 2a.
Is it a problem in maths or what?
Answer by Theo(13342) About Me  (Show Source):
You can put this solution on YOUR website!
no - there's no problem at all.

the simplified equation is a new and separate equation from the original equation it was derived from.

the domain of the simplified equation is different from the domain of the original equation.

there are rules for analyzing rational functions.

the simplified equation is useful to tell you whrere the asymptotes are.

but you can't expect the simplified equation to have the same undefined points as the original equation because it's a different equation that stands on its own.

an example:

find the vertical asymptotes for y = ((x-1)*(x+1))/((x-1)*(x+5))

y is undefined at x = 1 and x = -5, but there is a vertical asymptote only at x = -5.

here's the graph:



you can see from the graph that there is a vertical asymptote at x = -5.

what you can't see is that the value of the function is undefined at x = 1, but there is a hole there, even if there is no asymptote.

what has happened is that the (x-1) cancels out and you get the simplified equation that only has (x+5) in the denominator.

if the factor in the denominator cancels out when you simplify the eqaution, there is no vertical asymptote at that point.

if it doesn't cancel out, there is an asymptote at that point.

the following table will, however, show you that the value of the original equation is undefined at x = 1 and at x = -5, while the value of the simplified equation is only undefined at x = -5.

$$$

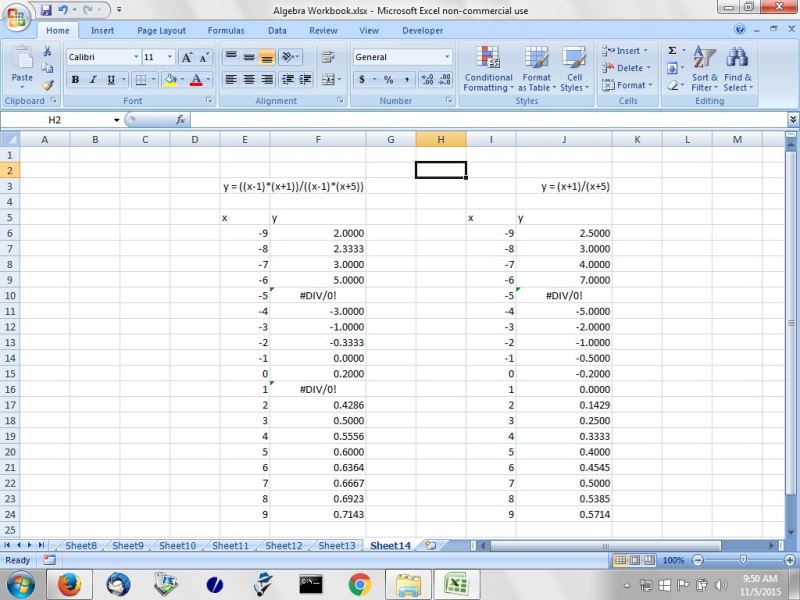
the original equation and the simplified equation are two different equations with two different domains.

the simplified equation is useful to tell you what the value of the hole is in the original equation.

here's some references that might help you to understand better.

http://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut40_ratgraph.htm

http://sites.csn.edu/istewart/mathweb/math126/graph_rational_func/graph_rational_func.htm