Question 1077969: Let A and B be the roots of an equation x2 +ax+b=0 and let C and D be the roots of x2+cx+d=0. Express (A-C) (B-C) (A-D) (B-D) in terms of the coefficients a, b,c ,d.
Answer by ikleyn(52835)   (Show Source):
You can put this solution on YOUR website! .
Let A and B be the roots of an equation x2 +ax+b=0 and let C and D be the roots of x2+cx+d=0.
Express (A-C) (B-C) (A-D) (B-D) in terms of the coefficients a, b,c ,d.
~~~~~~~~~~~~~~~~~~~~~~
1. (A-C)*(B-C) =  =  =  .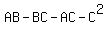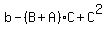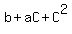
(I replaced here A+B by -a and replaced AB by b based on Vieta's formulas).
2. (A-D)*(B-D) =  =  =  .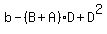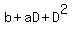
(Again, I replaced here A+B by -a and replaced AB by b based on Vieta's formulas).
3. Now (A-C)*(B-C)*(A-D)*(B-D) =  =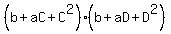
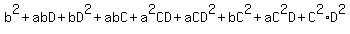=  = (regroup)
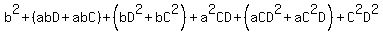=  = (simplify)
=  =
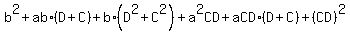(replace D+C = -c, 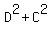 =  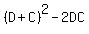= (-c)^2 -2d, CD = d, D+C = -c, (CD)^2 = d^2 based on Vieta's formulas. You will get)
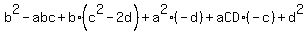=  = (simplify)
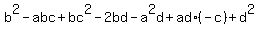=  = (I just got the expression via coefficients a, b, c and d !) =
=  =  .
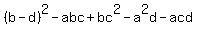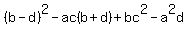Answer. (A-C)*(B-C)*(A-D)*(B-D) = .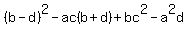
Lesson to learn from this solution:
This assignment is for those who firmly knows Vieta's formulas.
|
|
|
