Question 1041457: You have 23 coins totaling $2.75, how many quarters, nickles, and dimes do you have?
Found 4 solutions by josgarithmetic, purpleoj, MathTherapy, ikleyn:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! That will give you a system of equations in two equation with three unknown variables, and you know that the solution must be three whole numbers. Does that help?
Answer by purpleoj(8)   (Show Source): (Show Source):
You can put this solution on YOUR website! This question is actually impossible (at least if you want a solid answer.)
In order to solve it correctly, you would need three equations. However, this only gives you two, and, because of this, it doesn't provide enough information to solve.
However, you can solve for a variable, or check for more information. If you were given "The number of quarters equaled three times the number of dimes" or some other information, then this would be solvable.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You have 23 coins totaling $2.75, how many quarters, nickles, and dimes do you have?
Let number of quarters, dimes, and nickels be Q, D, and N, respectively
Then we get: Q + D + N = 23 -------- eq (i)
Also, .25Q + .1D + .05N = 2.75 ----- eq (ii)
Since there are a lot of coins worth only $2.75, there MUST be a small number of quarters. Therefore, we start with 1 quarter, but 1, 2, and 3
quarters DO NOT result in meaningful numbers of nickels, or dimes. However, 4 quarters do.
Let number of quarters be 4
Then we get: 4 + D + N = 23____D + N = 19 -------- eq (iii)
.25(4) + .1D + .05N = 2.75_____1 + .1D + .05N = 2.75____.1D + .05N = 1.75 ------- eq (iv)
- .1D - .1N = - 1.9 ----- Multiplying eq (iii) by - .1 ------- eq (v)
- .05N = - .15 ---------- Adding eqs (v) & (iv)
N, or number of nickels = 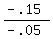 , or 3 , or 3
4 + D + 3 = 23 -------- Substituting 4 for Q and 3 for N in eq (i)
D + 7 = 23
D, or number of dimes = 23 – 7, or 16
This gives us: 
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You have 23 coins totaling $2.75, how many quarters, nickles, and dimes do you have?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
3 quarters, 20 dimes and 0 (zero) nickels also work . . .
|
|
|