Tutors Answer Your Questions about Word Problems With Coins (FREE)
Question 1209788: roberta has 4 dollars in dimes and quarters. She has 5 more dimes than quarters.In total, roberta has 25 coins
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how we can solve this problem:
Let $q$ be the number of quarters and $d$ be the number of dimes.
Since Roberta has 5 more dimes than quarters, we have the equation:
$d = q + 5$
The total number of coins is 25, so we have:
$q + d = 25$
Substituting the first equation into the second equation, we get:
$q + (q + 5) = 25$
Combining like terms, we have:
$2q + 5 = 25$
Subtracting 5 from both sides, we get:
$2q = 20$
Dividing both sides by 2, we find:
$q = 10$
Substituting this value back into the equation $d = q + 5$, we find:
$d = 10 + 5 = 15$
So, Roberta has 10 quarters and 15 dimes.
We can check our answer by verifying that the total amount of money is $4:
$0.25(10) + $0.10(15) = $2.50 + $1.50 = $4.00
Therefore, our answer is correct.
Question 1209144: wilson has 8 coins of same value and seven paise. Chloe has 11 coins of same value as those that wilson has and she has five paise. Wilson says "If you give me one of your coins and four paise, will have same amount of your money". What is the value of each coin that wilson and chloe have?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let x be the value of the unknown coins. Then
8x+7 = paise Wilson has
11x+5 = paise Chloe has
If Chloe gives Wilson one coin and 4 paise, then
(8x+7) + (x+4) = 9x+11 will be the paise Wilson has
(11x+5) - (x+4) = 10x+1 will be the paise Chloe has
Those two amounts will be the same
9x+11 = 10x+1
x=10
The value of the coins that Wilson and Chloe have is
ANSWER: 10 paise
Question 1209004: Quinn and Charlotte have been saving their coins and notes. Quinn has only saved
$2 coins and Charlotte only $5 notes.
Charlotte has 27 $5 notes and Quinn 76 $2 coins.
How much do they have together
Answer by ikleyn(52780)   (Show Source): (Show Source):
Question 1208876: In Stephen’s piggy bank there are as many nickels as pennies three more dimes the. Nickels and five fewer quarters than pennies. If he has 3.97 in his bank how many of each kind of coin does he have
Found 2 solutions by greenestamps, josgarithmetic:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The formal algebraic solution from the other tutor is fine. Note, however, that most students at any level will find it easier to work the problem in cents instead of dollars so that all the calculations are in whole numbers instead of decimals.
But you can get good problem-solving practice by solving a relatively simple problem like this using logical reasoning and simple arithmetic. Here are two such solutions.
(1) Changing the numbers of each kind of coin
Take away the three "extra" dimes so that the numbers of pennies, nickels, and dimes are all the same; that makes the total value of the coins $3.97 - $0.30 = $3.67.
Similarly, add five more quarters so that the numbers of all denominations of coins are the same. The new total value is $3.67 + $1.25 = $4.92. Let's change that to 492 cents to continue with the problem.
There are now equal numbers of pennies, nickels, dimes, and quarters. The value of one of each of those coins is 1+5+10+25 = 41 cents.
Divide the new total of 492 cents by 41 cents to find that there are 12 of each coin.
ANSWERS:
pennies: 12
nickels: 12
dimes (3 more than that): 15
quarters (5 fewer than that): 7
CHECK: 12(1) + 12(5) + 15(10) + 7(25) = 12+60+150+175 = 397 cents = $3.97
(2) Using logical reasoning, along with the given total value of $3.97 and the fact that the total value of the nickels, dimes, and quarters is a multiple of 5 cents, to solve the problem using "smart" trial and error.
With a total value of 397 cents, the number of pennies can only be 2, or 7, or 12, or 17, or....
There can't be only 2 pennies, because the number of quarters is 5 less than the number of pennies.
If there were 7 pennies, then the number of quarters would be only 7-5 = 2, and you aren't going to get a total of 397 cents with just 2 quarters.
Trying 12 pennies next, we find that gives us the correct total value of 397 cents.
From there the solution is the same as above.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1208422: if i had 1 $2, 1 $1, 4 50c, 5 20c and 5 10c coins what are the different ways I can make $2.00
Found 2 solutions by Edwin McCravy, greenestamps:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Use Excel or whatever computer program you have access to:
$2 $1 $0.50 $0.20 $0.10
1 0 0 0 0
0 1 2 0 0
0 1 1 2 1
0 1 1 1 3
0 1 1 0 5
0 1 0 5 0
0 1 0 4 2
0 1 0 3 4
0 0 4 0 0
0 0 3 2 1
0 0 3 1 3
0 0 3 0 5
0 0 2 5 0
0 0 2 4 2
0 0 2 3 4
0 0 1 5 5
Edwin
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Make an organized list using a "greedy" algorithm, in which you start your list with the largest possible numbers of the largest value coins.
(1) If you have the $2 coin, you are done -- you can't have any more coins.
(2) If you don't have the $2 coin, then you can have 2, 1, or 0 $1 coins.
(3) If you don't have the $2 or $1 coin, you can have 4, 3, 2, 1, or 0 50-cent coins.
(4) if you don't have any of the $2, $1, or 50-cent coins, you don't have enough other coins to make $2.
Make your list using that outline. I will do part of the work for you; you don't learn anything by having me do the whole problem for you.
$2 $1 50c 20c 10c case # from above
---------------------------------------------
1 0 0 0 0 (1)
0 2 0 0 0 (2)
0 1 2 0 0
0 1 1 2 1
0 1 1 1 3
0 1 1 0 5
0 1 0 5 0
0 1 0 4 2
0 1 0 3 4
0 0 4 0 0 (3)
0 0 3 ....... (3) (there are 3 solutions here)
0 0 2 ....... (3) (there are 3 solutions here)
0 0 1 ....... (3) (there is 1 solution here)
So there is a total of 17 solutions....
Question 1100355: Sam has $3.15 in quarters nickels and dimes he has half as many quarters as he has dimes and nickels together he also has two more nickels than dimes how many of each coin are there
Found 5 solutions by MathTherapy, Edwin McCravy, mccravyedwin, greenestamps, timofer:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Sam has $3.15 in quarters nickels and dimes he has half as many quarters as he has dimes and nickels together he also has two more nickels than dimes how many of each coin are there
Appears as though this should be written as:
"Sam has $3.15 in quarters, nickels, and dimes. He has half as many quarters as he has dimes and nickels, together.
He also has two more nickels than dimes. How many of each coin are there?"
Let number of dimes be D
Then number of nickels is D + 2 (He has 2 more nickels than dimes)
Number of quarters:  (He has half as many quarters
as he has dimes and nickels, together)
Amount in DIMES: .1D
Amount in NICKELS: .05(D + 2) = .05D + .1
Amount in QUARTERS: .25(D + 1) = .25D + .25
Total amount: $3.15
We then get: .1D + .05D + .1 + .25D + .25 = 3.15
.4D + .35 = 3.15
.4D = 2.8
Number of dimes, or (He has half as many quarters
as he has dimes and nickels, together)
Amount in DIMES: .1D
Amount in NICKELS: .05(D + 2) = .05D + .1
Amount in QUARTERS: .25(D + 1) = .25D + .25
Total amount: $3.15
We then get: .1D + .05D + .1 + .25D + .25 = 3.15
.4D + .35 = 3.15
.4D = 2.8
Number of dimes, or  Number of nickels: D + 2 = 7 + 2 = 9
Number of quarters: D + 1 = 7 + 1 = 8
Number of nickels: D + 2 = 7 + 2 = 9
Number of quarters: D + 1 = 7 + 1 = 8
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
In fact, you can even use artificial intelligence. You cannot trust AI for
advanced stuff, but it can solve simple stuff very easily. I copied and pasted
exactly word-for word what you posted above (without punctuation marks) into:
https://poe.com/
and here's what I got (copied and pasted) from that site:
-------------------------------------
Let's define the variables for the coins:
Let 𝑑 be the number of dimes.
Let 𝑛 be the number of nickels.
Let 𝑞 be the number of quarters.
From the problem, we have the following relationships:
The total value of the coins is $3.15, which is 315 cents:
10𝑑+5𝑛+25𝑞=315
Sam has half as many quarters as the total number of dimes and nickels:
𝑞=1/2(𝑑+𝑛)
He has two more nickels than dimes:
𝑛=𝑑+2
Now, we can substitute 𝑛 in terms of 𝑑 into the other equations.
From the third equation, we have: 𝑛=𝑑+2
Substituting 𝑛 into the second equation:
𝑞=(1/2)(𝑑+(𝑑+2))=(1/2)(2d+2)=d+1
Now substituting 𝑛 and 𝑞 into the first equation:
10𝑑+5(𝑑+2)+25(𝑑+1)=315
Expanding this gives:
10𝑑+5𝑑+10+25𝑑+25=315
40𝑑+35=315
Now, subtract 35 from both sides:
40𝑑=280
Dividing by 40:
𝑑=7
Now that we have d, we can find 𝑛 and 𝑞
𝑛=𝑑+2=7+2=9
𝑞=𝑑+1=7+1=8
Thus, the solution is:
Dimes (d): 7
Nickels (𝑛): 9
Quarters (𝑞): 8
Final Answer:
Dimes: 7
Nickels: 9
Quarters: 8
-------------------------
That was all copied and pasted exactly as poe.com printed instantly. But
don't depend on it for more advanced math. It will sometimes make stupid
mistakes. AI is not perfected yet. But someday it will be, and will take us
all over, just as Stephen Hawking warned. LOL (Maybe I shouldn't be laughing).
Edwin
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Apparently the younger generation doesn't see any need for punctuation marks or
capital letters to separate sentences. They just run them all together. And
soon the correct way to write will include "u" for "you", "r" for "are",
"before" as "b4", "8" for "ate", etc.
In that light, there are plenty of sites online where you only have to type in a
system of equations, point and click, and the answer pops out instantaneously.
So why not use them? You can even do it on a TI-84 calculator, if you install
the right program. Why hitch a horse to a buggy and get there in an hour, when
you can drive a car and get there in 10 minutes?
If you use a separate letter for each unknown, setting up the equations is a
cinch. This system below is set up directly from the words:
 Go to one of those sites. Type that in. Point and click, and instantly you
get q=8, d=7, n=9. Here is a link to such a site:
https://www.emathhelp.net/en/calculators/algebra-2/system-of-equations-solver/?
Edwin
Go to one of those sites. Type that in. Point and click, and instantly you
get q=8, d=7, n=9. Here is a link to such a site:
https://www.emathhelp.net/en/calculators/algebra-2/system-of-equations-solver/?
Edwin
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
He has two more nickels than dimes:
let x = # of dimes
then x+2 = # of nickels
He has half as many quarters as nickels and dimes together:
# of nickels and dimes together = x + (x+2) = 2x+2
# of quarters = (1/2)(2x+2) = x+1
The total value of the coins is $3.15, or 315 cents:
10(x)+5(x+2)+25(x+1)=315
10x+5x+10+25x+25=315
40x=280
x=280/40=7
ANSWERS:
nickels: x+2 = 9
dimes: x = 7
quarters: +1 = 8
CHECK: 9(5)+7(10)+8(25) = 45+70+200 = 315
Answer by timofer(104)  (Show Source): (Show Source):
You can put this solution on YOUR website! .
Go to
https://www.algebra.com/algebra/homework/word/coins/Word_Problems_With_Coins.faq.question.1100355.html
to see all the solutions.
Question 1207581: how do I find how many dimes he has?
Maurice has 280 coins - all quarters and dimes - won from playing poker. If his winnings
total $49.45, how many dimes does he have?"
and help for this please.
"The perimeter of a triangle is 64 metres. The longest side of the triangle is 3 times the
length of the shortest side, and the third side is 8 metres less than double the length of the
shortest side. Determine the dimensions of all three sides of the triangle."
Found 3 solutions by mananth, ikleyn, josgarithmetic:
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Maurice has 280 coins - all quarters and dimes - won from playing poker. If his winnings
total $49.45, how many dimes does he have?"
Let the number of dimes maurice has be d
and quarters be q
Maurice has 280 coins
d+q=280...........................................(1)
his winnings total $49.45
10d+25q=49.45*100.........................(2)
10d+25q=4945
multiply (1) by 10 and subtract from (2)
10d+10q= 2800
10d+25q=4945
15q= 2145
q= 2145/15 = 143
d+q= 280
Therefore d = 280-143=137
Maurice has 137 dimes.
Check
0.25×143+0.10×137=35.75+13.70=49.45
The perimeter of a triangle is 64 metres. The longest side of the triangle is 3 times the
length of the shortest side, and the third side is 8 metres less than double the length of the
shortest side. Determine the dimensions of all three sides of the triangle."
Let x be the longest side ,y be the shortest side and z the third side.
The longest side of the triangle is 3 times the
length of the shortest side,
x=3y ......................................(1)
The third side is 8 metres less than double the length of the
shortest side.
z= 2x-8 ..................................(2)
The perimeter of a triangle is 64 metres (given)
x+y+z= 64
x+(x/3)+(2x-8)=64
x+x/3 +2x-8=64
3x+x/3 = 72
multiply by 3
3x+3x = 216
6x=216
x= 36
x=3y
y=x/3
y = 36/3 = 12
x+y+z= 64
12+36+z= 64
z = 64-48
z= 16
The dimensions of the sides of the triangle are 12 meters, 36 meters, and 16 meters.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
help for this please.
"The perimeter of a triangle is 64 metres. The longest side of the triangle is 3 times the
length of the shortest side, and the third side is 8 metres less than double the length of the
shortest side. Determine the dimensions of all three sides of the triangle."
~~~~~~~~~~~~~~~~~~~
If you stop your analysis there, where @josgarithmetic stopped it, your solution
will be 100% incomplete and 100% incorrect.
As you read the problem, you may see that if x is the length of the shortest side
of the triangle, then
the longest side is 3x,
and the third side is 2x-8.
But such triangle can not exist, since the triangle inequality is violated.
Indeed, the sum of sides x and (2x-8) is 3x-8, and it is SHORTER than the length
of the third side, 3x, while, according to the triangle inequality, it should be LONGER
than the third side.
It means that the problem's condition is SELF-CONTRADICTORY and such a triangle CAN NOT exist.
Solved.
--------------------
The " solution " by @mananth is 100% incorrect.
It is " rotten to the core ", since a triangle with side lengths
12 meters, 16 meters and 36 meters does not exist.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1207580: how can i find the answer? Dave has eight more dimes than nickels in his pocket. In total, the coins in his pocket are
worth $3.05. How many of each type of coin does he have?
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
how can i find the answer? Dave has eight more dimes than nickels in his pocket.
In total, the coins in his pocket are worth $3.05. How many of each type of coin does he have?
~~~~~~~~~~~~~
Let x be the number of nickels; then the number of dimes is (x+8).
The value of nickels is 5x cents; the value of dimes is 10*(x+8) cents.
The total value is $3.05, or 305 cents; so we write this equation
5x + 10*(x+8) = 305.
Simplify and find x
5x + 10x + 80 = 305
15x = 305 - 80
15x = 225
x = 225/15 = 15.
ANSWER. 15 nickels and 15+8 = 23 dimes.
CHECK. The total value is 15*5 + 23*10 = 75 + 230 = 305 cents = $3.05. ! correct !
Solved.
Question 1205719: Katie has a collection of nickels, dimes and quarters with a total value of $6.80. There are 5 more dimes than nickels and 6 more quarters than nickels, how many of each coin does she have?
Found 4 solutions by MathTherapy, greenestamps, josgarithmetic, ikleyn:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Katie has a collection of nickels, dimes and quarters with a total value of $6.80. There are 5 more dimes than nickels and 6 more quarters than nickels, how many of each coin does she have?
Let number of nickels be N
Then, number of dimes and quarters = N + 5, and N + 6, respectively
Value of nickels: .05N
Value of dimes: .1(N + 5) = .1N + .5
Value of quarters:.25(N + 6) = .25N + 1.5
As total value is 6.80, we get: .05N + .1N + .5 + .25N + 1.5 = 6.8
.4N + 2 = 6.8
.4N = 4.8
Number of nickels, or  Now, calculate number of dimes (N + 5), and number of quarters (N + 6).
Now, calculate number of dimes (N + 5), and number of quarters (N + 6).
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
You can solve the problem informally, using steps that are nearly the same as the formal algebraic solution shown by the other tutor.
Probably this problem was supposed to be solved using formal algebra; but you can get good mental exercise solving the problem without it.
The value of the 5 "extra" dimes is 5($0.10) = $0.50; the value of the 6 "extra" quarters is 6($0.25) = $1.50. The total value of those "extra" coins is $0.50 $1.50 = $2.00.
So the value of the remaining coins is $6.80 - $2.00 = $4.80.
Those coins are equal numbers of nickels, dimes, and quarters. The total value of a group consisting of one nickel, one dime, and one quarter is $0.40. To make the remaining $4.80, the number of those groups must be $4.80/$0.40 = 12.
So the number of nickels is 12; the number of dimes is 12+5 = 17, and the number of quarters is 12+6 = 18.
ANSWERS: 12 nickels, 17 dimes, 18 quarters
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Katie has a collection of nickels, dimes and quarters with a total value of $6.80.
There are 5 more dimes than nickels and 6 more quarters than nickels, how many of each coin does she have?
~~~~~~~~~~~~~~~~~~~~~~
Let x be the number of nickels;
then the number of dimes is (x+5) and the number of quarters is (x+6).
Write the total money equation in cents
5x + 10*(x+5) + 25*(x+6) = 680 cents.
Simplify and find x
5x + 10x + 50 + 25x + 150 = 680
5x + 10x + 25x = 680 - 50 - 150
40x = 480
x = 480/40 = 12.
ANSWER. There are 12 nickels, 12+5 = 17 dimes and 12+6 = 18 quarters.
CHECK. 12*5 + 17*10 + 18*25 = 680 cents, total. ! correct !
Solved.
Question 1205731: 50 coins in dimes and quarters have a total value of $11.00. How many dimes and quarters are there?
Found 2 solutions by greenestamps, josgarithmetic:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Informally....
If all 50 coins were dimes, the total value would be $5.00.
The actual total value is $11.00, which is $6.00 more.
Since each quarter is worth $0.15 more than each dime, the number of quarters must be $6.00/$0.15 = 600/15 = 40.
ANSWER: 40 quarters and 10 dimes
CHECK: 40($0.25)+10($0.10) = $10.00+$1.00 = $11.00
----------------------------------------------------------------------
And here is a really unorthodox solution, treating the problem as a mixture problem.
You are mixing quarters worth 25 cents each with dimes worth 10 cents each to get a mixture of coins worth an average of $11.00/50 = 22 cents each.
Since 22 cents is 4/5 of the way from 10 cents to 25 cents, 4/5 of the coins must be quarters. (From 10 to 25 is a difference of 15; from 10 to 22 is a difference of 12; 12/15 = 4/5.)
4/5 of 50 is 40.
ANSWER (again, of course): 40 quarters and 10 dimes
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1205611: How many pennies are needed to make $3.75?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
Question 1205515: Consider the event of getting a head in 4tosses of a fair coin. Let X be the random variable representing the number of heads minus the number of tails. Create a Probability Distribution table for the random variable X.
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
The probability distribution is
| # heads | # tails | X = heads-tails | P(X) | | 4 | 0 | 4 | 1/16 | | 3 | 1 | 2 | 4/16 | | 2 | 2 | 0 | 6/16 | | 1 | 3 | -2 | 4/16 | | 0 | 4 | -4 | 1/16 |
Below I'll explain how I got each P(X) probability value.
There are n = 4 tosses of the coin.
That gives 2^n = 2^4 = 16 different outcomes.
Of those outcomes, there's only one way to get all heads. Same goes for all tails. That explains the 1/16 probability values for the first and last rows.
If there are 3 heads, then there are 4 ways to have this situation. This is because there are 4 places to put the tail. Those 4 outcomes are:- HHHT
- HHTH
- HTHH
- THHH
Due to symmetry, the same idea applies if there are 3 tails.
So that's how we get a probability of 4/16 for the 2nd row and 2nd to last row.
If there are 2 heads, then there are 4C2 = 6 ways to arrange them. The 4C2 refers to the nCr combination formula. Such values can be found in Pascal's Triangle. The 6 ways to have 2 heads and 2 tails are listed here- HHTT
- HTTH
- HTHT
- TTHH
- THTH
- THHT
So that's how I'm getting 6/16 for the probability of 2 heads.
I have not reduced the fractions in the P(X) column because I wanted to keep the denominators the same. But if you wanted you could reduce the fractions.
4/16 = 1/4
6/16 = 3/8
Or you can convert all the fractions to decimal form.
1/16 = 0.0625
4/16 = 1/4 = 0.25
6/16 = 3/8 = 0.375
Each decimal value is exact.
Two things to notice:- Each P(X) value is between 0 and 1.
- The P(X) values add to 1.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The statement of the problem is faulty.
The event of getting a head in 4 tosses of a fair coin is a single event. "A head" means there is one head, so there are 3 tails, and the number of heads minus the number of tails is 1-3 = -2.
So the very uninteresting probability distribution is
P(-2) = 1
Question 1205537: Lucas has 37 coins, all nickels and dimes in his piggy bank. The value of the coins is $3.10. How many dimes does Lucas have?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The typical formal algebraic solution shown by the other tutor is of course fine; you should understand it and be able to solve similar problems by that method.
For a mental solution method....
Note that if all 37 coins were dimes the total value would be $3.70.
That is $0.60 more than the actual total of $3.10.
Since each nickel is worth $0.10-$0.05 = $0.05 less than each dime, the number of nickels must be $0.60/$0.05 = 60/5 = 12.
Therefore the number of dimes is 37-12 = 25
ANSWER: 25
Note this method can be used to solve a wide range of similar problems quickly, without formal algebra.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Lucas has 37 coins, all nickels and dimes in his piggy bank.
The value of the coins is $3.10. How many dimes does Lucas have?
~~~~~~~~~~~~~~~~~~~
D dimes; (37-D) nickels.
Write the total money equation
10*D + 5*(37-D) = 310 cents.
Solve it and find D
10*D + 5*37 - 5*D = 310
10*D - 5*D = 310 - 5*37
5*D = 125
D = 125/5 = 25.
ANSWER. 25 dimes.
Solved.
Question 1205418: If Zaire has 4 times as many quarters as dimes and they have a combined value of $4.40, how many of each coin does he have?
Found 4 solutions by josgarithmetic, Edwin McCravy, MathLover1, ikleyn:
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
1 group of 4 quarters and 1 dime is worth $1.10.
$4.40 is 4 of those groups.
So there are 4x4=16 quarters and 1x4=4 dimes.
Edwin
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
If Zaire has 4 times as many quarters as dimes and they have a combined value
of $4.40, how many of each coin does he have?
~~~~~~~~~~~~~~~~~~~~~~
Group the coins in sets containing 4 quarters and 1 dime.
Each group is worth 4*25 + 10 = 110 cents.
In all, there are 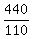 = 4 such groups.
ANSWER. There are 4*4 = 16 quarters and 4 dimes. = 4 such groups.
ANSWER. There are 4*4 = 16 quarters and 4 dimes.
Solved.
------------------
The grouping method is a perfect way to solve such problems MENTALLY.
See the lessons
- Solving coin problems mentally by grouping without using equations
- Santa Claus helps solving coin problem
in this site.
Find there many similar problems solved and learn both the method and the subject at the same time !
Question 1205410: Marie has 39 quarters and nickels. The total value is $ 5.15.
Write an equation and solve for how many quarters and nickels she has.
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Marie has 39 quarters and nickels. The total value is $ 5.15.
Write an equation and solve for how many quarters and nickels she has.
~~~~~~~~~~~~~~~~~~~~~
Let Q be the number of quarters.
Then the number of nickels is (39-Q).
Write the total money equation, in cents
25Q + 5*(39-Q) = 515 cents.
Simplify and find Q
25Q + 5*39 - 5Q = 515
25Q - 5Q = 515 - 5*39
20Q = 320
Q = 320/20 = 16.
ANSWER. 16 quarters and 39-16 = 23 nickels.
CHECK. 25*16 + 5*23 = 515 cents, in total. ! correct !
Solved.
---------------------
For introductory coin problems, look into the lessons
- Coin problems
- More Coin problems
- Solving coin problems without using equations
- Kevin and Randy Muise have a jar containing coins
in this site.
Read them attentively and become an expert in this field.
Question 1205276: Erica has 4 dimes, 3 nickels, and 4 pennies. How much money does she have?
Found 5 solutions by Alan3354, josgarithmetic, ikleyn, math_tutor2020, Edwin McCravy:
Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
One of our tutors answered such questions this way:
- If you can not solve it mentally on your own, you should not go out.
And that's fair.
------------------
Probably, true destination of this problem is to train an artificial intelligence by feeding its memory.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Similar question: A person has 6 dimes, 5 nickels and 4 pennies. How much money do they have?
Solution:
6 dimes = 6*10 = 60 cents
5 nickels = 5*5 = 25 cents
4 pennies = 4*1 = 4 cents
total = 60+25+4 = 89 cents = $0.89
Keep in mind that this isn't the answer to your particular question, since I changed the numbers around, but the process/outline is the same.
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website! Erica has 4 dimes,That's 4 10-cent pieces. Can you multiply 4 times 10 to see how many
cents that is? 3 nickels,That's 3 5-cent pieces. Can you multiply 3 times 5 to see how many
cents that is? and 4 pennies.
That's 4 1-cent pieces. Can you multiply 4 times 1 to see how many
cents that is? How much money does she have?If you were able to do the above difficult tasks, can you also do the
extremely difficult task of adding those together?
I actually believe you can do all those difficult calculations all by
yourself, if you try hard enough.
Edwin
Question 1204965: A 5.2 horsepower pump can move 345 lbs of water against a discharge head of 300 feet. What is the horsepower of a pump that moves 434 lbs of water against a discharge head off 400 feet
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A 5.2 horsepower pump can move 345 lbs of water against a discharge head of 300 feet. What is the horsepower
of a pump that moves 434 lbs of water against a discharge head off 400 feet
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As the problem is worded, printed and presented, it is posed INCORRECTLY.
To be correct, the problem must say in the second scenario "in the same time".
It is a KEY PART of the problem's condition, and without it, the problem CAN NOT be solved.
Alas, it is quite obvious that the author/(composer of this problem)
does not know Physics and does not know the relevant basic conceptions.
Therefore, I should perform his duties here and make his job instead of him.
I would advise to the problem's composer to take very beginning class in Physics,
which they usually teach in middle school in 6-th/7-th grade in Science.
====================
Hello, the goal of this forum is to teach students to solve problems.
It assumes, that the visitors bring problems that are posed correctly.
The goal of this forum is not to teach mathematically illiterate
persons how to compose/create Math problems correctly.
Question 1204793: Annie has a piggy bank consisting of quarters dimes and nickels. She has a total 74 coins in the bank totaling 11.35$. There are half as many dimes as quarters. How many nickels does Annie have?
Found 2 solutions by math_tutor2020, josgarithmetic:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
"There are half as many dimes as quarters" which flips around to "There are twice as many quarters as dimes".
# of quarters = 2*(# of dimes)
Let x = number of dimes
2x = number of quarters
x+2x = 3x = number of dimes and quarters
Annie has 74 coins total.
3x of them are either quarters or dimes, so the remaining 74-3x coins must be nickels.
x = number of dimes
10x = value of the dimes in cents
2x = number of quarters
25*2x = 50x = value of the quarters in cents
74-3x = number of nickels
5*(74-3x) = 370 - 15x = value of the nickels in cents
total value in cents = 10x+50x+370-15x = 45x+370
Set this equal to the total amount Annie has which is 1135 cents (aka $11.35)
45x+370 = 1135
45x = 1135-370
45x = 765
x = 765/45
x = 17
So,
number of dimes = x = 17
number of quarters = 2x = 2*17 = 34
number of nickels = 74-3x = 74-3*17 = 23
In short,
number of dimes = 17
number of quarters = 34
number of nickels = 23
Check
17 dimes + 34 quarters + 23 nickels = 17*10 + 34*25 + 23*5 = 1135 cents = $11.35
This helps confirm the answer.
Further confirmation comes from the fact that 17+34+23 = 74
Answer: She has 23 nickels
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1204794: Annie has a piggy bank consisting of quarters dimes and nickels. She has a total 74 coins in the bank totaling 11.35$. There are half as many dimes as quarters. How many nickels does Annie have?
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1204685: write the expression as a equation Jody has 2 more nickels than pennies, and she has 30 coins all together
Found 3 solutions by josgarithmetic, greenestamps, ikleyn:
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A couple of comments about the response from tutor @ikleyn....
Actually, "all together" is better English than "altogether", although many native English speakers will use "altogether".
The formal meaning of "altogether" is different -- as in "now you are talking about something altogether different".
And for "2 more nickels than pennies", the most direct translation into an algebraic equation is n = p+2. The equation n-p=2 that she uses is equivalent; but it doesn't directly translate the words as they are given.
----------------------------------------------------------------
The comment from tutor @ikleyn about my comment regarding "altogether" and "all together" clearly demonstrates her character: she believes she is never wrong about anything.
If you read the things she writes, it is obvious that it is ludicrous for her to be teaching what is proper English.
If you rearrange the statement "she has 30 coins all together" to read "all together, she has 30 coins", then it is clear that "all together" is correct.
I tried to make my comment as pleasant as possible, stating that "all together" was BETTER English than "altogether", but with her omniscient attitude, she had to claim that MY English was incorrect.
So pitiful and sad....
Answer by ikleyn(52780)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
write the expression as a equation Jody has 2 more nickels than pennies, and she has 30 coins all together
~~~~~~~~~~~~~~~~~~~
In this context, write one word  instead of two separate words all together. instead of two separate words all together.
Let N be the number of nickels
and let P be the number of pennies.
Write equations as you read the problem
N - P = 2 (1) "2 more nickels than pennies"
N + P = 30 (2) "30 coins altogether"
Since you ask about writing equations, at this point I completed my answer.
--------------------
Memorize this instruction " Write equations as you read the problem ".
These words are MAGIC. They will help you to write system of equations
in many other problems in your life.
Always write equations as you read the problem.
If you do not know how to write equations, read the problem again.
Do it until the problem will itself tell you how to write equations.
In real life, nobody will help you, until you find your own right way.
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
For your information
ALTOGETHER - - - meaning (from a dictionary)
completely; totally.
including everything or everyone; in total.
taking everything into consideration; on the whole.
ALL TOGETHER - - - meaning (from a dictionary)
all in one place or in a group; all at once.
Notice that the dictionary interpretation of " altogether " is different from that of @greenestamps
(has nothing in common).
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110
|




