Question 967015: One cube has each of its faces covered by one face of an identical cube, making a solif as shown. The volume of the solid is 875 cm cubed.
What, in cm squared, is the surface area of the solid?
A 750
B 800
C 875
D 900
E 1050
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The solid is not shown, but anyone who ever rolled dice knows that a cube has 6 faces,
so attaching one cube to each face of the original cube,
we end up with a cluster of  cubes. cubes.
 , so if the solid volume is , so if the solid volume is 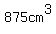 , ,
the volume of the each cube (the original cube and the other 6 identical ones) is
 . .
Since the volume of a cube is the cube of the edge length,
the length of the edge of those cubes, in cm, is  . .
The surface area of a face of a cube with edge length 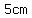 is is
 . .
In the 7 cube cluster, none of the 6 faces of the original cube is visible (all are covered).
The other 6 identical cubes attached to the original cube have one face covered (attached to the original cube,
so each one has  exposed faces. exposed faces.
The total exposed surface of the 7-cube cluster consists of
 cube faces (5 faces from each of 6 cubes). cube faces (5 faces from each of 6 cubes).
So the total surface area is 
|
|
|