|
Question 955746: The areas of two similar tetrahedrons are 24 sq. in. and 96 sq. in. Find the ratio of their volumes.
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the formula for the area and volume of a tetrahedron is shown below
http://www.vitutor.com/geometry/solid/surfacevolume_formulas.html
the area of a tetrahedron is equal to s^2 * sqrt(3).
the volume of a tetrahedron is equal to s^3 * sqrt(2) / 12.
in the reference, they call the length of the side equal to a.
in this presentation, i call the length of the side equal to s.
i used s because i use a to mean the area and i use v to mean the volume and i therefore use s to mean the side.
let A1 = area of smaller tetrahedron.
let A2 = area of larger tetrahedron.
let s1 = side of smaller tetrahedron.
let s2 = side of larger tetrahedron.
formula for the area of the smaller tetrahedron is A1 = (s1)^2 * sqrt(3)
solve for s1 and you get s1 = sqrt(A1/sqrt(3))
formula for the area of the larger tetrahedron is A2 = (s2)^2 * sqrt(3)
since A2 = 4*A1, then 4*A1 = (s2)^2 * sqrt(3)
solve for s2 to get s2 = sqrt(4*A1/sqrt(3)) which can be simplified to:
s2 = 2 * sqrt(A1/sqrt(3))
you have:
s1 = sqrt(A1/sqrt(3)) and you have s2 = 2 * sqrt(A1/sqrt(3)).
this means that s2 = 2*s1.
so, when A2 = 4*A1, s2 = 2*s1.
we can now find the volume of A1 and A2.
the formula for volume is V = s^3 * sqrt(2) / 12
volume of A1 is therefore equal to (s1)^3 * sqrt(2) / 12.
volume of A2 is therefore equal to (s2)^3 * sqrt(2) / 12.
since we know that s2 = 2*s1, then:
volume of A2 is equal to (2*a1)^3 * sqrt(2) / 12.
simplify this to get volume of A2 is equal to 8*(a1)^3 * sqrt(2) / 12.
we have:
volume of A1 is equal to (s1)^3 * sqrt(2) / 12.
volume of A2 is equal to 8*(a1)^3 * sqrt(2) / 12.
volume of A2 is therefore equal to 8 times the volume of A1.
that's your solution.
the ratio of the volume of the larger tetrahedron to the volume of the smaller tetrahedron is equal to 8/1.
the ratio of the area of the larger tetrahedron to the area of the smaller tetrahedron is equal to 4/1.
the ratio of the length of the side of the larger tetrahedron to the length of the side of the smaller tetrahedron is equal to 2/1.
this is consistent with the general rule for 3 dimensional figures.
the general rule for 3 dimensional figures states:
the ratio of the areas is equal to the ratio of the sides squared and the ratio of the volumes is equal to the ratio of the sides cubed.
since the ratio of the areas is equal to the ratio of the sides squared, this means that the ratio of the sides is equal to the square root of the ratio of the areas.
in algebraic terms, this looks like this:
s means side
a means area
v means volume
s2/s1 is the ratio of the sides.
a2/a1 is the ratio of the areas.
v2/v1 is the ratio of the volumes.
tetrahedron 2 is the larger tetrahedron.


from  , you can solve for , you can solve for  to get: to get:

from  , you can replace , you can replace  with with 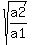 to get: to get:

the ratio of the volumes of the two tetrahedrons is equal to the (square root of the ratio of the areas) cubed.
the ratio of the area is equal to 96/24 = 4
the ratio of the volume is equal to (sqrt(4))^3 which is equal to 2^3 = 8.
|
|
|
| |