|
Question 1181730: The center of each of three spheres of radius R lies in the surfaces of the other two. Pass a plane containing the centers of the spheres. Find the area common to the three great circles cut from the spheres by this plane.
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
1. **Visualize the Setup:** Imagine three spheres, each with its center on the surface of the other two. The plane containing the centers cuts each sphere along a great circle (a circle with radius R). We're looking for the area where all three great circles overlap.
2. **The Triangle:** The centers of the three spheres form an equilateral triangle. Since each center is on the surface of the other two spheres, and all spheres have the same radius R, the side length of this equilateral triangle is 2R.
3. **The Great Circles:** The plane cutting through the centers creates three great circles. Because the centers form an equilateral triangle, these great circles intersect each other at 60-degree angles.
4. **The Common Area:** The area common to all three great circles forms an equilateral triangle in the center. To find the area of this triangle, we need to know its side length.
5. **Finding the Side Length:** Let's call the side length of the central equilateral triangle 's'. Consider one of the 60-degree sectors of a great circle. The central equilateral triangle cuts off 1/3 of each 60-degree angle, or 20 degrees. The side length of the equilateral triangle is related to the radius R by the law of cosines.
s² = R² + R² - 2R²cos(60°)
s² = 2R² - 2R²(1/2) = R²
s = R
6. **Area of the Central Triangle:** The area of an equilateral triangle with side length 's' is given by (s²√3)/4. In our case, s = R.
Area = (R²√3)/4
Therefore, the area common to the three great circles is (R²√3)/4.
Answer by ikleyn(52794)  (Show Source):
You can put this solution on YOUR website! .
The center of each of three spheres of radius R lies in the surfaces of the other two.
Pass a plane containing the centers of the spheres.
Find the area common to the three great circles cut from the spheres by this plane.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill, the solution is INCORRECT conceptually;
therefore, his calculations are incorrect and his answer is incorrect, too.
The major fault is that his description and understanding of the common area
of intersecting great circles of the spheres is incorrect.
See my solution below.
The centers of the three great circles form an equilateral triangle.
The sides of this triangle are of the length R, since R is the radius of each
of the three spheres.
The area of this triangle is a =  .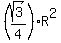
But the common intersection area is  than this triangle.
The common area is formed as the intersection of three  of the great circles,
each sector with the central angle of 60°.
So, the common area can be described as the equilateral triangle with the sides length of R
 three adjacent circular SEGMENTS adjacent to each side of this triangle.
The area of each such a segment is b =  - .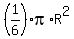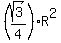
The area of the three such segments is 3b =  -  .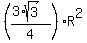
Therefore, the total common area of the intersection of the three great circles is
Area = a + 3b = + - =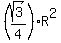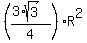
= -  = -  =
=  .
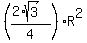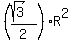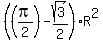ANSWER. The common area of intersection of the three great circles is ,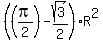
or about 0.6998*R^2, approximately.
Solved.
Compare it with the answer by @Phill of 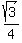 = 0.433*R^2 (approximately).
////////////////////////////
Regarding the post by @CPhill . . .
Keep in mind that @KPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, in my view, doing this way, this guy, @CPhill, simply makes dishonest business at this forum.
Every time, @CPhill embarrasses to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
|
|
|
| |
