|
Tutors Answer Your Questions about Volume (FREE)
Question 1210251: I iron pipe has a cross section, the iron being 1cm thick. The mass of 1cm3 of cast iron is 7.2g. Calculate the mass of a 2metre length of the pipe
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There is not enough information to get an answer.
In addition to knowing the length of the pipe and the thickness of the iron, we need to know either the inside or outside diameter (or radius) of the pipe.
Re-post, showing all the required information.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I iron pipe has a cross section, the iron being 1cm thick.
The mass of 1cm3 of cast iron is 7.2g.
Calculate the mass of a 2metre length of the pipe
~~~~~~~~~~~~~~~~~~~~~~~~~~
To solve the problem, multiply the cast iron density of 7.2 g/cm^3 by the volume of the metal.
To find the volume of the metal, multiply the cross-section area of the pipe by its length
in consistent units.
To find the area of the cross-section of the pipe, from the greater area of the circle subtract
the area of the smaller circle.
To find the areas of circles in cross-section, the radii or diameters are needed
(since the thickness of the pipe is given, any one of the two radii/diameters should be given).
But neither radius nor diameter of the pipe is given in the post, making the problem like
a three-leg horse.
I am very disappointed by inaccuracy of the person, who created this three-leg horse problem
and disseminates it in the Internet.
It is inappropriate level to communicate with the tutors, posting them crippled tasks.
Question 1168325: The volume of the water in a hemisphere having a radius of 2 m is 2.05 cu. m. Find the height of the water. It says in our book that the height should be 0.602 m.
I have already tried solving it but I got lost in the middle. I hope you can help me with this. Thank you!
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1181731: A sphere is inscribed in a right circular cone of altitude h and radius of base r. Write a formula in terms of r and h for the volume of the sphere.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A sphere is inscribed in a right circular cone of altitude h and radius of base r.
Write a formula in terms of r and h for the volume of the sphere.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
After attentive reading the solution by @CPhill, I see the errors in it,
that require me to fix them.
So, I copy the solution by @CPhill and make my editing right there.
Here's how to derive the formula for the volume of the inscribed sphere in terms of *r* and *h*:
**1. Diagram and Key Relationships:**
Draw a cross-section of the cone and sphere. You'll see a circle (representing the sphere) inscribed in a triangle (representing the cone).
* Let *R* be the radius of the inscribed sphere.
* The radius of the cone's base is *r*.
* The height (altitude) of the cone is *h*.
* The slant height of the cone (the hypotenuse of the triangle) is *s* = sqrt(r² + h²).
**2. Similar Triangles:**
There are two similar right triangles in the cross-section:
* The large triangle representing the cone, with sides *r*, *h*, and *s*.
* A smaller triangle formed by the radius of the sphere (*R*), the difference between the cone's height and the sphere's radius (*h - R*), and a portion of the slant height.
The ratio of corresponding sides in similar triangles is equal:
R / r = (h - R) / s
**3. Solve for R:**
R / r = (h - R) / sqrt(r² + h²)
R * sqrt(r² + h²) = r(h - R)
R * sqrt(r² + h²) = rh - rR
R * sqrt(r² + h²) + rR = rh
R(sqrt(r² + h²) + r) = rh
R = rh / (sqrt(r² + h²) + r)
**4. Rationalize the Denominator (Optional but often preferred):**
Multiply the numerator and denominator by the conjugate of the denominator:
R = rh(sqrt(r² + h²) - r) / ((sqrt(r² + h²) + r)(sqrt(r² + h²) - r))
R = rh(sqrt(r² + h²) - r) / (r² + h² - r²)
R = rh(sqrt(r² + h²) - r) / h <<<---===  : should be R = rh(sqrt(r² + h²) - r) / h²
R = r(sqrt(r² + h²) - r) <<<---=== as a consequence, should be R = r(sqrt(r² + h²) - r)/h
otherwise, the 'R's dimension is m^2, instead of 'm'.
**5. Volume of the Sphere:**
The volume *V* of a sphere is given by:
V = (4/3)πR³
Substitute the expression for *R* we derived:
V = (4/3)π[r(sqrt(r² + h²) - r)/h]³ <<<---=== associated correction here
Therefore, the volume of the inscribed sphere in terms of *r* and *h* is:
V = (4/3)πr³(sqrt((r² + h²) - r)/h)³ <<<---=== associated correction here : should be R = rh(sqrt(r² + h²) - r) / h²
R = r(sqrt(r² + h²) - r) <<<---=== as a consequence, should be R = r(sqrt(r² + h²) - r)/h
otherwise, the 'R's dimension is m^2, instead of 'm'.
**5. Volume of the Sphere:**
The volume *V* of a sphere is given by:
V = (4/3)πR³
Substitute the expression for *R* we derived:
V = (4/3)π[r(sqrt(r² + h²) - r)/h]³ <<<---=== associated correction here
Therefore, the volume of the inscribed sphere in terms of *r* and *h* is:
V = (4/3)πr³(sqrt((r² + h²) - r)/h)³ <<<---=== associated correction here
Now everything is correct.
In previous version by @CPhill, even the dimensions of the expressions were wrong.
//////////////////////////////////////////
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-paste that of Google.
Every time, @CPhill embarrasses to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX
Dear @CPhill, I will include such comment to every your post, where I will find an error,
UNTIL you will place a correct acknowledgment in every your post.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to derive the formula for the volume of the inscribed sphere in terms of *r* and *h*:
**1. Diagram and Key Relationships:**
Draw a cross-section of the cone and sphere. You'll see a circle (representing the sphere) inscribed in a triangle (representing the cone).
* Let *R* be the radius of the inscribed sphere.
* The radius of the cone's base is *r*.
* The height (altitude) of the cone is *h*.
* The slant height of the cone (the hypotenuse of the triangle) is *s* = sqrt(r² + h²).
**2. Similar Triangles:**
There are two similar right triangles in the cross-section:
* The large triangle representing the cone, with sides *r*, *h*, and *s*.
* A smaller triangle formed by the radius of the sphere (*R*), the difference between the cone's height and the sphere's radius (*h - R*), and a portion of the slant height.
The ratio of corresponding sides in similar triangles is equal:
R / r = (h - R) / s
**3. Solve for R:**
R / r = (h - R) / sqrt(r² + h²)
R * sqrt(r² + h²) = r(h - R)
R * sqrt(r² + h²) = rh - rR
R * sqrt(r² + h²) + rR = rh
R(sqrt(r² + h²) + r) = rh
R = rh / (sqrt(r² + h²) + r)
**4. Rationalize the Denominator (Optional but often preferred):**
Multiply the numerator and denominator by the conjugate of the denominator:
R = rh(sqrt(r² + h²) - r) / ((sqrt(r² + h²) + r)(sqrt(r² + h²) - r))
R = rh(sqrt(r² + h²) - r) / (r² + h² - r²)
R = rh(sqrt(r² + h²) - r) / h
R = r(sqrt(r² + h²) - r)
**5. Volume of the Sphere:**
The volume *V* of a sphere is given by:
V = (4/3)πR³
Substitute the expression for *R* we derived:
V = (4/3)π[r(sqrt(r² + h²) - r)]³
Therefore, the volume of the inscribed sphere in terms of *r* and *h* is:
V = (4/3)πr³(sqrt(r² + h²) - r)³
Question 1181729: The diameter of a sphere coincides with the axis of a right circular cone, and the surface of the cone intersects the surface of the sphere in in a great circle. Find: (a) the vertical angle of the cone: (b) the volume of the cone; (c) the volume common to the two solids: (d) the volume of that portion of the cone which lies outside the sphere: (e) the volume of that portion of the sphere which lies outside the cone. Denote radius of sphere by R.
Solve Problem if (a) R=2: (b) R=3.72.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The diameter of a sphere coincides with the axis of a right circular cone, and the surface
of the cone intersects the surface of the sphere in in a great circle. Find:
(a) the vertical angle of the cone:
(b) the volume of the cone;
(c) the volume common to the two solids:
(d) the volume of that portion of the cone which lies outside the sphere:
(e) the volume of that portion of the sphere which lies outside the cone. Denote radius of sphere by R.
Solve Problem if (a) R=2: (b) R=3.72.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill is INCORRECT.
It is incorrect, since @CPhill incorrectly interprets the problem.
He solves the problem in assumption that the cone TOUCHES the sphere
along a great circle.
But, firstly, it is  , and, secondly, the problem , and, secondly, the problem  something something  . .
It says that the cone' surface  the sphere surface at the great circle, the sphere surface at the great circle,
which is totally different condition.
Thus, the value of @CPhill' solution is ZERO.
He is just deceiving you.
//////////////////////////
Regarding the post by @CPhill . . .
Keep in mind that @KPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, in my view, doing this way, this guy, @CPhill, simply makes dishonest business at this forum.
Every time, @CPhill embarrasses to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Special note for a visitor who posted this problem.
It borders on madness to pack 5 (five) questions into one post.
The rules of this forum allow one question per post.
Even if assume that the rules are made of rubber, then 3 questions per post is the maximum.
Every time, as you violate this rule, you EITHER will wait several years, OR will get a mess.
Regarding the rules of this forum, see this page
https://www.algebra.com/tutors/students/ask.mpl?action=ask_question&topic=Equations&return_url=http://www.algebra.com/algebra/homework/equations/
from which you post your problems.
It is assumed that you read these rules before posting.
It is also assumed that you do understand what is written in that page and follow the rules.
Those who violate them, work against their own interests.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the solution, broken down step by step:
**1. Visualize the Setup:** Imagine a sphere perfectly nestled inside a cone, with the sphere's diameter matching the cone's axis. The sphere touches the cone along a great circle.
**2. Key Geometric Relationships:**
* Let *R* be the radius of the sphere.
* The cone's height (h) is equal to the sphere's diameter, so h = 2R.
* The slant height (s) of the cone is the distance from the apex to any point on the edge of the circular base.
* The radius of the cone's base (r) can be found using the Pythagorean theorem.
**3. (a) Vertical Angle of the Cone:**
* Consider a right triangle formed by the cone's height (2R), the cone's radius (r), and the cone's slant height (s). Half of the cone's vertical angle (θ/2) is the angle between the slant height and the axis (height).
* sin(θ/2) = r / s
* Since the sphere touches the cone along a great circle, r = R.
* s = sqrt(r² + h²) = sqrt(R² + (2R)²) = sqrt(5R²) = R√5
* sin(θ/2) = R / (R√5) = 1/√5
* θ/2 = arcsin(1/√5)
* θ = 2 * arcsin(1/√5) ≈ 51.83°
**4. (b) Volume of the Cone:**
* Volume of a cone = (1/3)πr²h
* V_cone = (1/3)πR²(2R) = (2/3)πR³
**5. (c) Volume Common to the Two Solids:**
* The volume common to both is simply the volume of the sphere.
* V_common = (4/3)πR³
**6. (d) Volume of the Cone Outside the Sphere:**
* V_outside_sphere = V_cone - V_common
* V_outside_sphere = (2/3)πR³ - (4/3)πR³ = (-2/3)πR³
**Important Correction:** The volume of the cone *outside* the sphere should be a positive value. We made an error in the calculation. It should be:
V_outside_sphere = V_cone - V_common
V_outside_sphere = (2/3)πR³- (4/3)πR³
Question 1181730: The center of each of three spheres of radius R lies in the surfaces of the other two. Pass a plane containing the centers of the spheres. Find the area common to the three great circles cut from the spheres by this plane.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The center of each of three spheres of radius R lies in the surfaces of the other two.
Pass a plane containing the centers of the spheres.
Find the area common to the three great circles cut from the spheres by this plane.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
In the post by @CPhill, the solution is INCORRECT conceptually;
therefore, his calculations are incorrect and his answer is incorrect, too.
The major fault is that his description and understanding of the common area
of intersecting great circles of the spheres is incorrect.
See my solution below.
The centers of the three great circles form an equilateral triangle.
The sides of this triangle are of the length R, since R is the radius of each
of the three spheres.
The area of this triangle is a = 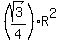 .
But the common intersection area is .
But the common intersection area is  than this triangle.
The common area is formed as the intersection of three than this triangle.
The common area is formed as the intersection of three  of the great circles,
each sector with the central angle of 60°.
So, the common area can be described as the equilateral triangle with the sides length of R of the great circles,
each sector with the central angle of 60°.
So, the common area can be described as the equilateral triangle with the sides length of R
 three adjacent circular SEGMENTS adjacent to each side of this triangle.
The area of each such a segment is b = three adjacent circular SEGMENTS adjacent to each side of this triangle.
The area of each such a segment is b = 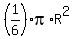 - - 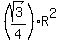 .
The area of the three such segments is 3b = .
The area of the three such segments is 3b =  - - 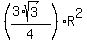 .
Therefore, the total common area of the intersection of the three great circles is
Area = a + 3b = .
Therefore, the total common area of the intersection of the three great circles is
Area = a + 3b = 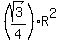 + +  - - 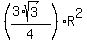 =
= =
=  - - 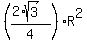 = =  - - 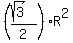 =
= =
= 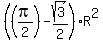 .
ANSWER. The common area of intersection of the three great circles is .
ANSWER. The common area of intersection of the three great circles is 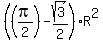 ,
or about 0.6998*R^2, approximately. ,
or about 0.6998*R^2, approximately.
Solved.
Compare it with the answer by @Phill of 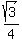 = 0.433*R^2 (approximately). = 0.433*R^2 (approximately).
////////////////////////////
Regarding the post by @CPhill . . .
Keep in mind that @KPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, in my view, doing this way, this guy, @CPhill, simply makes dishonest business at this forum.
Every time, @CPhill embarrasses to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
1. **Visualize the Setup:** Imagine three spheres, each with its center on the surface of the other two. The plane containing the centers cuts each sphere along a great circle (a circle with radius R). We're looking for the area where all three great circles overlap.
2. **The Triangle:** The centers of the three spheres form an equilateral triangle. Since each center is on the surface of the other two spheres, and all spheres have the same radius R, the side length of this equilateral triangle is 2R.
3. **The Great Circles:** The plane cutting through the centers creates three great circles. Because the centers form an equilateral triangle, these great circles intersect each other at 60-degree angles.
4. **The Common Area:** The area common to all three great circles forms an equilateral triangle in the center. To find the area of this triangle, we need to know its side length.
5. **Finding the Side Length:** Let's call the side length of the central equilateral triangle 's'. Consider one of the 60-degree sectors of a great circle. The central equilateral triangle cuts off 1/3 of each 60-degree angle, or 20 degrees. The side length of the equilateral triangle is related to the radius R by the law of cosines.
s² = R² + R² - 2R²cos(60°)
s² = 2R² - 2R²(1/2) = R²
s = R
6. **Area of the Central Triangle:** The area of an equilateral triangle with side length 's' is given by (s²√3)/4. In our case, s = R.
Area = (R²√3)/4
Therefore, the area common to the three great circles is (R²√3)/4.
Question 1181724: 17. Find the volume of the largest right circular cylinder of altitude 8 in. that can be cut from a sphere of diameter 12 in.
Found 2 solutions by greenestamps, CPhill:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There largest right circular cylinder with height 8 that can be cut from a sphere with diameter 12 is the cylinder that can be inscribed in the sphere.
For that cylinder, each base is 8/2 = 4 units from the center of the sphere. Then, from the Pythagorean Theorem, with the radius of the sphere being 6, the radius of each base of the cylinder is 2*sqrt(5).
And then the volume of the cylinder is

ANSWER: 160pi
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the volume of the largest cylinder:
**1. Visualize the Setup:** Imagine a sphere with a cylinder inside it. The cylinder's height is fixed at 8 inches, and we want to find the largest possible radius for the cylinder.
**2. Key Dimensions:**
* Sphere diameter = 12 inches, so sphere radius (R) = 6 inches.
* Cylinder height (h) = 8 inches.
* Let 'r' be the radius of the cylinder.
**3. Cross-Section:** A cross-section through the center of the sphere and cylinder reveals a circle (the sphere) with a rectangle (the cylinder) inside. The diagonal of this rectangle is the diameter of the sphere (12 inches).
**4. Pythagorean Theorem:** We can use the Pythagorean theorem to relate the sphere's radius (R), the cylinder's radius (r), and *half* of the cylinder's height (h/2):
R² = r² + (h/2)²
**5. Solve for the Cylinder's Radius (r):**
6² = r² + (8/2)²
36 = r² + 16
r² = 20
r = √20 = 2√5 inches
**6. Volume of the Cylinder:**
Volume of a cylinder = πr²h
V = π(2√5)² * 8
V = π * 20 * 8
V = 160π cubic inches
**Therefore, the volume of the largest right circular cylinder is 160π cubic inches, or approximately 502.65 cubic inches.**
Question 1181727: A cone is inscribed in a sphere. It has for its base a great circle of the sphere and for its vertex a pole of that circle. Find the ratio (a) of the total area of the cone to the area of the sphere, (b) of the volume of the cone to the volume of the sphere.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the ratios:
**1. Visualize the Setup:** Imagine a sphere. The cone's base is a great circle (a circle with the sphere's radius), and the cone's tip (vertex) is at one of the poles (farthest points from the great circle).
**2. Key Dimensions:**
* Let *R* be the radius of the sphere.
* The radius of the cone's base (r) is equal to the sphere's radius: r = R.
* The height (h) of the cone is also equal to the sphere's radius: h = R.
* The slant height (s) of the cone can be found using the Pythagorean theorem: s = sqrt(r² + h²) = sqrt(R² + R²) = R√2
**3. (a) Ratio of Total Area of Cone to Area of Sphere:**
* Area of the cone's base = πr² = πR²
* Lateral surface area of the cone = πrs = πR(R√2) = πR²√2
* Total surface area of the cone = Area of base + Lateral surface area = πR² + πR²√2 = πR²(1 + √2)
* Surface area of the sphere = 4πR²
Ratio of areas = [πR²(1 + √2)] / (4πR²) = (1 + √2) / 4
**4. (b) Ratio of Volume of Cone to Volume of Sphere:**
* Volume of the cone = (1/3)πr²h = (1/3)πR²R = (1/3)πR³
* Volume of the sphere = (4/3)πR³
Ratio of volumes = [(1/3)πR³] / [(4/3)πR³] = 1/4
**Summary of Ratios:**
* (a) Ratio of total area of cone to area of sphere: (1 + √2) / 4
* (b) Ratio of volume of cone to volume of sphere: 1/4
Question 1181746: A spherical ball of radius R is dropped into a vessel in the form of an inverted right circular cone. Find the radius and altitude of the cone, if when three more balls each of radius R are dropped into it they from a layer on top of the first ball such that all four balls are tangent to each other and in addition each ball of the upper layer is tangent both to the side and to the top of the vessel.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to analyze this problem and determine if there are any solutions:
**1. Visualize the Setup:** Imagine the cone with the four spheres inside. The first sphere sits at the bottom, and the other three rest on top of it, forming a small pyramid. Crucially, all spheres are tangent to each other and the cone.
**2. Key Geometric Relationships:**
* **Tangency:** The centers of tangent spheres are separated by a distance equal to twice their radius (2R).
* **Cone and Sphere:** The centers of the three upper spheres form an equilateral triangle. The distance from the center of any of these spheres to the apex of the cone is related to the cone's dimensions and the sphere's radius.
**3. Analyze the Vertical Distances:**
* The center of the bottom sphere is at a height R from the cone's apex.
* The centers of the upper spheres are at a height 3R from the cone's apex (R from the apex to the center of the bottom sphere, plus 2R separating the centers of the bottom and top spheres).
**4. The Crucial Condition:**
The problem states that the upper spheres are tangent to the *top* of the vessel. This is where the issue arises. For the top spheres to be tangent to the top of the vessel, the top of the vessel must be at the same height as the top of the spheres. The top of the spheres is located at a height 4R from the apex of the cone (3R from the apex to the center of the top spheres, plus R from the center to the top).
**5. The Contradiction:**
For the three top spheres to also be tangent to the *sides* of the cone, the angle of the cone must be such that the spheres can fit snugly. The height of the cone required for three spheres of radius R to be tangent to each other and the sides of the cone is *less than* 4R. The condition that the spheres must be tangent to the *top* of the vessel forces the height to be 4R. These two requirements are incompatible.
**6. Conclusion:**
There are *no* solutions for the radius and altitude of the cone that satisfy all the given conditions. The requirement that the top spheres be tangent to both the sides and the top of the vessel creates a geometric contradiction.
Question 1181748: A diameter of a sphere of radius R coincides with an element of a right circular cylinder of diameter R. For the solid common to the sphere and the cylinder, find the area of a section made by (a) a plane containing the axis of the cylinder and the diameter of the sphere which coincides with the element of the cylinder, (b) the plane perpendicular to the axis of the cylinder at its midpoint, (c) a plane containing the axis of the cylinder and perpendicular to the plane of (a).
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the area of the sections:
**1. Visualize the Problem:** Imagine a sphere and a cylinder intersecting. The cylinder's diameter is equal to the sphere's radius, and one of the cylinder's sides (an element) is aligned with a diameter of the sphere. The common solid is the region where both the sphere and cylinder exist.
**2. Define Coordinate System:** It's helpful to use a coordinate system. Let the axis of the cylinder and the diameter of the sphere be along the z-axis. The center of the sphere is at the origin (0,0,0).
**a) Plane Containing the Axis and the Diameter:**
* This plane is essentially a cross-section through the center of both the sphere and the cylinder.
* The intersection with the sphere is a circle of radius R.
* The intersection with the cylinder is a rectangle with height 2R (the diameter of the sphere) and width R (the diameter of the cylinder).
* The section of the common solid is the *smaller* of these two shapes, which is the rectangle.
* Area of the rectangle = height * width = 2R * R = 2R²
**b) Plane Perpendicular to the Axis at Midpoint:**
* This plane is horizontal (parallel to the x-y plane) and passes through the center of the sphere (z = 0).
* The intersection with the sphere is a circle of radius R.
* The intersection with the cylinder is a circle of radius R/2.
* The section of the common solid is the smaller circle, which is the intersection with the cylinder.
* Area of the circle = π * (radius)² = π * (R/2)² = (πR²)/4
**c) Plane Containing the Axis and Perpendicular to the Plane in (a):**
* This plane is perpendicular to the plane in (a). It's effectively a vertical plane passing through the center of the cylinder.
* The intersection with the sphere is a circle of radius R.
* The intersection with the cylinder is a rectangle with height 2R and width R.
* The section of the common solid is again the smaller of the two, which will be two rectangles, each with height 2R and width R/2.
* Total area of the two rectangles = 2 * (height * width) = 2 * (2R * R/2) = 2R²
**Summary of Areas:**
* (a) Plane containing the axis and the diameter: 2R²
* (b) Plane perpendicular to the axis at midpoint: (πR²)/4
* (c) Plane containing the axis and perpendicular to the plane in (a): 2R²
Question 1181750: A cylinder of radius a pass centrally through a sphere of radius r. Show that the volume removed from the sphere is the difference of two spheres one of radius r and the other of radius r cos θ, where sin θ= a/r.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's the proof that the volume removed from the sphere is the difference of two spheres:
**1. Visualize the Problem:** Imagine the cylinder passing through the sphere. The removed volume is a cylindrical "tunnel" with curved ends. We'll find this volume by integrating.
**2. Set up the Integral:**
* Consider a thin horizontal slice of the sphere at a height *z* from the center. This slice is a circle.
* The radius of this circular slice (let's call it *x*) can be found using the Pythagorean theorem: x² + z² = r². So, x = √(r² - z²).
* However, the cylinder removes a central portion of this circle. The "kept" parts of the circular slice are two segments, and the removed part is what's inside the cylinder. The width of this removed part is 2y, where y can be found using the Pythagorean theorem in the cross-section of the cylinder: y² + z² = a². So, y = √(a² - z²). Note that this equation is only valid for |z| <= a.
* The area of the removed part of the circular slice is 2y*√(r² - z²) = 2√(a² - z²)*√(r² - z²).
* To find the total removed volume, we integrate this area from -a to a:
V_removed = ∫(from -a to a) 2√(a² - z²)*√(r² - z²) dz
**3. Trigonometric Substitution:**
Let z = r*sin(θ). Then dz = r*cos(θ)*dθ. When z = a, sin(θ) = a/r, so θ = arcsin(a/r). Let's call this angle θ₀. When z = -a, sin(θ) = -a/r, so θ = -arcsin(a/r) = -θ₀.
Now substitute:
V_removed = ∫(from -θ₀ to θ₀) 2√(a² - r²sin²θ)*√(r² - r²sin²θ) * r*cos(θ)*dθ
V_removed = 2r²∫(from -θ₀ to θ₀) cos²θ*√(a² - r²sin²θ) dθ
Since a = rsin(θ₀),
V_removed = 2r²∫(from -θ₀ to θ₀) cos²θ*√(r²sin²θ₀ - r²sin²θ) dθ
V_removed = 2r³∫(from -θ₀ to θ₀) cos²θ*cosθ*√(sin²θ₀ - sin²θ) dθ
V_removed = 2r³∫(from -θ₀ to θ₀) cos³θ*√(sin²θ₀ - sin²θ) dθ
This integral is quite complex. Instead, let's consider a different approach.
**4. Alternative Approach (Geometric):**
The volume removed is the volume of the cylinder plus the volume of the two spherical caps at the ends.
* **Volume of the cylinder:** V_cyl = πa² * 2√(r² - a²) = 2πa²√(r² - a²)
* **Volume of each spherical cap:** The volume of a spherical cap of height h and radius r is given by (πh²/3)(3r - h).
* The height of each cap is h = r - √(r² - a²).
* V_cap = (π(r - √(r² - a²))²/3)(3r - (r - √(r² - a²)))
* V_cap = (π(r - √(r² - a²))²/3)(2r + √(r² - a²))
* Total volume of the two caps = 2V_cap.
* **Total removed volume:** V_removed = V_cyl + 2V_cap
This expression is also quite complex.
**5. The key insight:** The volume removed can also be calculated as the difference between the volume of the sphere of radius r and the volume of a sphere of radius rcosθ, where sinθ = a/r.
* Volume of sphere of radius r: (4/3)πr³
* Volume of sphere of radius rcosθ: (4/3)π(rcosθ)³
* Difference: (4/3)πr³ - (4/3)πr³cos³θ = (4/3)πr³(1 - cos³θ)
This approach is significantly simpler. While the integral approach is valid, this geometric insight provides a much easier way to express the volume removed.
**Conclusion:**
The volume removed from the sphere is indeed the difference of the volumes of two spheres, one with radius *r* and the other with radius *rcosθ*, where *sinθ = a/r*. This is a result of the geometry of the intersection.
Question 1209433: A solid rectangular prism with sides of 8cm by 12cm by 16cm is painted brown and then cut into 1cm^3 cubes. How many of the small cubes are painted on just one side?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A solid rectangular prism with sides of 8cm by 12cm by 16cm is painted brown
and then cut into 1cm^3 cubes. How many of the small cubes are painted on just one side?
~~~~~~~~~~~~~~~~~~~~~~~~
We have six basic faces 8*12 (two), 8*16 (two) and 12*16 (two).
Small cubes that are painted on just one side, are those cubes that have one small face
on the basic surfaces listed above, one strip away from their edges.
So, the numbers of such small cubes is
2*(8-2)*(12-2) + 2*(8-2)*(16-2) + 2*(12-2)*(16-2) = 2*6*10 + 2*6*14 + 2*10*14 = 568.
ANSWER. The number of such small cubes is 568.
Solved.
Question 1208875: A bowl with radius 30 cm , shaped like a hemisphere, is filled with water to two-thirds its depth. What is the surface area of the water, in cm²?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A bowl with radius 30 cm , shaped like a hemisphere, is filled with water
to two-thirds its depth. What is the surface area of the water, in cm²?
~~~~~~~~~~~~~~~~~~~
The total depth of the bowl is the radius of 30 cm (given).
Two-thirds of the total depth is 2/3 of 30 cm, i.e. 20 cm.
Hence, 10 cm is over the water surface.
Thus the square of the radius of the water surface in the bowl is (from Pythagoras)
r^2 = 30^2 - 10^2 = 900 - 100 = 800 cm^2
Hence, the surface area of the water in the bowl is
 = = 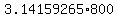 = 2513.27412 cm^2, or 2513.27 cm^2 (rounded). ANSWER = 2513.27412 cm^2, or 2513.27 cm^2 (rounded). ANSWER
Solved.
Question 1207756: In tetrahedron ABCO,angle AOB = angle AOC = angle BOC = 90degree.A cube is inscribed in the tetrahedron so that one of its vertices is at O,and the opposite vertex lies on face ABC.Let a = OA, b = OB,and c = OC.$ Show that the side length of the cube is
abc/(ab + ac + bc)
Answer by Alan3354(69443)   (Show Source): (Show Source):
Question 1207330: Container A was filled with water to the brim. Then, some of the water was
poured into an empty Container B until the height of the water in both
containers was the same. Find the new height in both water containers.
Dimensions of container A: height=40, length= 25, width= 30
Dimensions of container B: height= unknown, length=25, width=18
Found 4 solutions by Edwin McCravy, ikleyn, greenestamps, mananth:
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
 When container A was filled with water to the brim, the volume of water in it
was lwh=(25)(30)(40).
Then, some water from A was poured into B (when B was empty), until the height
of the water in both containers was the same.
Let that common height be the unknown x.
So the height of the water in A went down from 40 to x. Therefore the volume
of water in A was reduced to lwh=(25)(30)x.
and
the height of the water in B went up from 0 to x. Therefore the volume of water
in B went up from 0 to lwh=(25)(18)x.
Then the sum of the volumes of water in both containers afterward was the same
amount of water as was in container A at the beginning, so we have an equation:
(25)(30)x + (25)(18)x = (25)(30)(40)
Solve that for x and you'll get the correct answer.
[Note. You may connect this problem to something you may have learned in your
science class as to how to get the water levels the same. Although the problem
says the water was 'poured' from A to B, a better (or at least more scientific)
way to get the levels the same would be to use a siphon. A siphon is a water-
filled tube connecting the water in the two containers. The water at the bottom
of A must support the heavy weight of all the water above it, so the upper water
in A will "push down" on the lower water in A forcing water to flow up the tube
from A into B. The heavy upper water in A will continue to "push down" on the
lower water in A, forcing water up the tube from A into B, until the water
levels are the same.]
Edwin
When container A was filled with water to the brim, the volume of water in it
was lwh=(25)(30)(40).
Then, some water from A was poured into B (when B was empty), until the height
of the water in both containers was the same.
Let that common height be the unknown x.
So the height of the water in A went down from 40 to x. Therefore the volume
of water in A was reduced to lwh=(25)(30)x.
and
the height of the water in B went up from 0 to x. Therefore the volume of water
in B went up from 0 to lwh=(25)(18)x.
Then the sum of the volumes of water in both containers afterward was the same
amount of water as was in container A at the beginning, so we have an equation:
(25)(30)x + (25)(18)x = (25)(30)(40)
Solve that for x and you'll get the correct answer.
[Note. You may connect this problem to something you may have learned in your
science class as to how to get the water levels the same. Although the problem
says the water was 'poured' from A to B, a better (or at least more scientific)
way to get the levels the same would be to use a siphon. A siphon is a water-
filled tube connecting the water in the two containers. The water at the bottom
of A must support the heavy weight of all the water above it, so the upper water
in A will "push down" on the lower water in A forcing water to flow up the tube
from A into B. The heavy upper water in A will continue to "push down" on the
lower water in A, forcing water up the tube from A into B, until the water
levels are the same.]
Edwin
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let x be the volume in A after pouring into B
Let y be the volume in B after pouring
Full volume in A = L*w*h =30000
x+y =30000
Volume in A after pouring
x = A*h
x = h*25*30
x = 750h
h = x/750
Volume in B = h *25*18
y = 450h
h= y/450
Heights are same after pouring
x/750 = y/450
x = y*750/450
x = 5y/3
x+y =30000 ( full volume in A)
substitute x
5y/ 3 + y = 30000
8y/3 = 30000
8y = 90000
y = 90000/8
y=11250 ( Volume in B after pouring)
x = 30000-11250
x=18750 (volume in A after pouring)
Volume / area = h
18750/750 = 25
Volume in B = 30000-18750 =11250
h= 11250/450 =25
Height same after pouring
Question 1207300: A company that manufactures dog food wishes to pack in closed cylindrical tins.
What should be the dimensions of each tin if it is to have a volume of 128πcm³
and the minimum possible surface area?
Found 4 solutions by MathLover1, Edwin McCravy, greenestamps, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
Answer by greenestamps(13200)   (Show Source): (Show Source):
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A company that manufactures dog food wishes to pack in closed cylindrical tin's as,
what should be the dimensions of each tin if it is to have a volume of 128π cm³
and the minimum possible surface area.
~~~~~~~~~~~~~~~~~~~~~~~~~~~
As you know, the volume of a cylinder is
V = 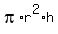 ,
where pi = 3.14, r is the radius and h is the height.
In your case the volume is fixed: ,
where pi = 3.14, r is the radius and h is the height.
In your case the volume is fixed:
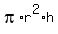 = =  cm^3. (1)
The surface area of a cylinder is
S = cm^3. (1)
The surface area of a cylinder is
S = 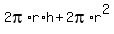 , (2)
and they ask you to find minimum of (2) under the restriction (1).
Using (1), I can rewrite (2) in the form
S(r) = , (2)
and they ask you to find minimum of (2) under the restriction (1).
Using (1), I can rewrite (2) in the form
S(r) = 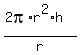 + +  = = 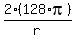 + +  = = 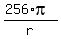 + +  . (3)
The plot below shows the function S(r) = . (3)
The plot below shows the function S(r) = 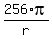 + +  , and you can clearly see that it has the minimum. , and you can clearly see that it has the minimum.
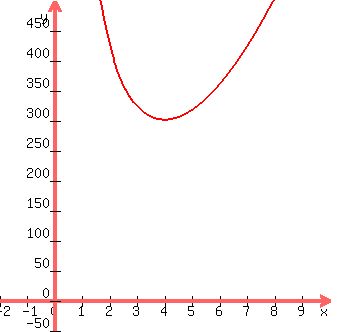 Plot y =
Plot y = 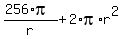 To find the minimum, use Calculus: differentiate the function to get
S'(r) =
To find the minimum, use Calculus: differentiate the function to get
S'(r) = 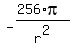 + + 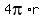 = = 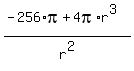 and equate it to zero.
S'(r) = 0 leads you to equation
and equate it to zero.
S'(r) = 0 leads you to equation 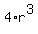 = =  , which gives
r = , which gives
r = 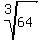 = 4 cm.
Answer. r = 4 cm, h = = 4 cm.
Answer. r = 4 cm, h = 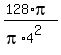 = 8 cm gives the minimum of the surface area. = 8 cm gives the minimum of the surface area.
Solved.
Question 1207242: A cylindrical can holds three tennis balls. each ball has a diameter of 6 cm, which is the same diameter as the cylinder, and the cylinder is filled to the top. Calculate the volume of space in the cylinder not taken up by the tennis balls. Round to the nearest cubic centimeter
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1207238: what is the depth of water in a can, if the cylindrical can has a base area of 15 centimetre square and contains 225 centimetre cube
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1207207: A small glass pyramid is packaged inside a box. The pyramid has a length and width of 2 inches and a height of 4 inches. the box is 5in x 5in x 5in how much will be left inside the box to put bubble wrap
Answer by ikleyn(52781)   (Show Source): (Show Source):
Question 1096524: A chemist needs to store a liquid inside a container in a laboratory room. She is trying to determine whether to store the liquid in a regular square pyramid or in a right circular cone storage container. The pyramid container has a base that is 6 inches by 6 inches and a height of 8 inches. The cone container has a base with a diameter of 6 inches and a height of 10 inches. Which container --the pyramid or the cone -- has a greater volume, and by how many cubic inches?
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Volume of square pyramid = a^2 * h/3
a= 6*6=36 in^2
h=8 in
V= 36*8/3 = 96 in^3
Volume of cone = 1/3 pi r^2 h
r=3, h= 10 in
V= 1/3 * pi * 3^2 *10 =94.25 in^3
The square pyramid container has a greater volume by 96−94.25=1.75 in^3
Question 1080457: What is the value of x in the linear inequality?
-3(4x-8.2)<-11.98x+14 3/4
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! -3*(4x-8.2)<-11.98x+(59/4)
expand
-12x +24.6< -11.98x+59/4
-12x +24.6-24.6 < -11.98x+59/4-24.6
-12x < -11.98x+59/4-24.6
-12x < -11.98x-9.85
-12x +11.98x< -11.98x-9.85+11.98x
-0,02x<-9.85
x >9.85/0.02
x>492.5
Question 1076433: a right pyramid 6 meter high has a square base of which the diagonal is root 1152 meter . volume of the pyramid is
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! a right pyramid 6 meter high has a square base of which the diagonal is root 1152 meter . volume of the pyramid is
Diagonal of square base sqrt(1152)
Let side of base be x m
x^2+x^2= 1152
2x^2= 1152
x^2=576
x=24
Volume of pyramid
1/3* a^2*h
1/3*24^2*6 =1152 m^3
Question 1098602: A concrete gate post comprises a right rectangular prism .length of sides of a rectangular prism (having a square base and a pyramid on top) is 30cm and the height of the rectangular section is 150cm. perpendicular height of the pyramid section is 8cm. What is the volume of concrete required to make ONE post?
Surface area of the pyramid section of the post?
If the length of sides of base is halved, how many posts,having the same design can be made with the same volume of concrete as the original post
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Volume of pyramid = 1/3 *s^2*h
V= 1/3 *30^2*8= 2400 cm^3
Volume of cylindrical portion l*b*h
V= 30*30*150= 135000 cm^3
TOTAL volume =137400 cm^3
Surface area of the pyramid section of the post=4 pi r l
4*area of one triangle
4*1/2 *30*17=1020 cm^2
The base is reduced by 1/2 - prism
If the edges are halved they will become 15 cm each. Volume now will be (15*15*150
=33750 cm^3
pyramid volume
1/3*15*15*8=600 cm^3
prism volume = 15*15*150=34350 cm^3
Number of posts =137400/34350 =4 posts from the same volume of concrete
Question 1125543: The volume of ice-cream in the cone is half the volume of the cone. The cone has a 3 cm radius and height of 14 cm. What is the depth of the ice-cream, correct to 2 decimal places?
Found 2 solutions by ikleyn, mananth:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The volume of ice-cream in the cone is half the volume of the cone.
The cone has a 3 cm radius and height of 14 cm. What is the depth of
the ice-cream, correct to 2 decimal places?
~~~~~~~~~~~~~~~~~~~
In this problem, there is no need to calculate volumes of the cones.
The cone volumes ratio is 2 (the greater to the smaller);
hence, from similarity of the cones, the ratio of heights (greater to smaller) is 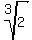 = 1.26 (rounded).
So, the depth of the ice-cream is = 1.26 (rounded).
So, the depth of the ice-cream is 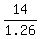 = 11.11 cm. ANSWER = 11.11 cm. ANSWER
Solved, as simple and in a way as it should be done.
---------------
By the way, the given radius of the greater cone of 3 cm is irrelevant.
This value is excessive, is not necessary, and the problem can be solved without it . . .
The answer to the question does not depend on the radius of the greater cone
and is the same for any other value of the radius of the greater cone.
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
From fig:
r/h = 3/14
r=3h/14
Volume of cone = 1/3 * pi*r^2*h
Plug values r=3 and h=14
V=132 in^3
Icecream is half volume of cone
V ice cream =66 in^3
r= 3h/14
substitute in cone volume formula
66= (1/3)*(22/7)*(3h/14)^2*h
198*7/22 = (9h^2/196)*h
63= (9h^2/196)*h
63*196/9 = h^3
7*196=h^3
h=11.11 cm height/depth of ice cream
 . .
Question 1166470: From a cylindrical object of diameter 70cm and height 84cm a right solid cone having is base as one of circular ends of the cylinder and with height 84cm is removed.calculate the area of the remaining solid object and calculate the remaining solid object (take pia radius to be 22/7)
Found 2 solutions by ikleyn, mananth:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! From a cylindrical object of diameter 70cm and height 84cm a right solid cone having is base as one of circular ends of the cylinder and with height 84cm is removed.calculate the area of the remaining solid object and calculate the remaining solid object (take pia radius toOOps
Deleted as error pointed out by@Ikleyn. Thanks
Question 1137425: Abigail is putting juice into cone - shaped containers to make popsicle's. She has approximately one quarter of a gallon, or 58 cubic inches, of juice to make the popsicle's with. Each container has a height of 3 inches.
Use the information to complete the table indicating the maximum number of popsicle's that Abigail could make with 58 cubic inches of juice.
Radius of the
Container
0.5 inch
1 inch
1.5 inch
What is the maximum number of popsicle's per container?
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Abigail is putting juice into cone - shaped containers to make popsicle's. She has approximately one quarter of a gallon, or 58 cubic inches, of juice to make the popsicle's with. Each container has a height of 3 inches.
Use the information to complete the table indicating the maximum number of popsicle's that Abigail could make with 58 cubic inches of juice.
Radius of the
Container
0.5 inch
1 inch
1.5 inch
What is the maximum number of popsicle's of each size
Volume of container = 1/3 *pi*r^2*h
radius =0.5 in
height = 3 inches
Quantity she has is 58 in^3
V=(1/3)*pi*(0.5)^2*3=0.785 in^3 per popsicle
Number of popsicles = 58/0.785 =73.88
So 73 popsicles from the quantity she has with her
repeat for other sizes
Question 1206272: What is 5ftx6.4ftx8ftx8ftx8ft???? i had it and it was really hard
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Never in my long life I saw meaningful problem where such calculations would need to be made
and where the dimension ft^5 would arise.
It is just somewhere beyond common sense, in a parallel (or perpendicular) Universe.
For future generations of students, who will read this post, my advise is do not take it seriously.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1206110: A rectangular swimming pool is 7 3⁄4 meters long, 4 1⁄3 meters wide, and 1 3⁄4 meters deep. What is the volume of the swimming pool?
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1205453: A heavy 9cm diameter ball is placed in an empty cylindrical tin of diameter 12cm. Enough water is poured into the can to cover the ball. If the ball is then removed, how far does the water level fall?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
diameter of the ball = 9
radius = diameter/2 = 9/2 = 4.5
A = volume of the ball
A = (4/3)*pi*r^3
A = (4/3)*pi*(4.5)^3
A = 121.5pi
diameter of cylinder container = 12
r = radius = diameter/2 = 12/2 = 6
The water level is h = 9 so that it reaches the top of the 9 cm diameter ball.
B = combined volume of the ball and surrounding water in the cylinder
B = pi*r^2*h
B = pi*6^2*9
B = 324pi
C = volume of water only
C = difference of volumes A and B
C = B - A
C = 324pi - 121.5pi
C = 202.5pi
Use the value of C to compute the new height of the water level after the ball is removed.
The cylinder's radius r = 6 will stay the same.
V = pi*r^2*h
202.5pi = pi*6^2*h
202.5pi = 36pi*h
h = (202.5pi)/(36pi)
h = 5.625
The water level is 5.625 cm after the ball is removed.
This assumes no water spills out.
The water line started at 9 cm and now is at 5.625 cm
This is a difference of 9 - 5.625 = 3.375 cm which represents how far the water line dropped.
This converts to the mixed number 3 & 3/8 aka 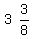 since 3/8 = 0.375 exactly. since 3/8 = 0.375 exactly.
Answer in decimal form 3.375 cm
Answer as a mixed number: 3 & 3/8 cm or 3 3/8 cm
Question 1205354: a rectangular tank 50 cm long and 25 cm wide contains 12 litres of water. when 4 metal cubes of the same size are placed in the tank, the height of the water level becomes 10 cm. what is the length of each edge of the cube?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a rectangular tank 50 cm long and 25 cm wide contains 12 litres of water.
when 4 metal cubes of the same size are placed in the tank, the height
of the water level becomes 10 cm. what is the length of each edge of the cube?
~~~~~~~~~~~~~~~~~~~~~
After submerging the 4 metal cubes in the tank, the volume occupied by the water
and cubes together is 50*25*10 = 12500 cm^3.
Hence, the volume of the 4 metal cubes is 12500 - 12*1000 = 500 cm^3.
Thus the volume of each of the 4 metal cubes is 500/4 = 125 cm^3.
The size of each cube is  = 5 cm. ANSWER = 5 cm. ANSWER
Solved.
---------------
The major lesson which a student should learn from this post is that this problem is SIMPLE.
The second major lesson which a student should learn is on HOW TO solve this simple problem by a simple way.
Question 1205355: a tin contains 8 litre of oil. 3/4 of the oil was poured into an empty rectangular container with a base area of 300 cm^2. if the container was 5/6 filled at the end, find the height of the container.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a tin contains 8 litre of oil. 3/4 of the oil was poured into an empty rectangular container
with a base area of 300 cm^2. if the container was 5/6 filled at the end, find the height of the container.
~~~~~~~~~~~~~~~~~~~~~
3/4 of 8 liters is 6 liters, or 6000 cm^3.
The height of the oil in the container with the base os 300 cm^2 is 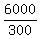 = 20 cm.
Since these 20 cm are 5/6 od the container height, hence
the container height is = 20 cm.
Since these 20 cm are 5/6 od the container height, hence
the container height is 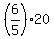 = 6*4 = 24 cm. ANSWER = 6*4 = 24 cm. ANSWER
Solved.
-------------------
The major lesson which a student should learn from this post is that this problem is SIMPLE.
The second major lesson which a student should learn is on HOW TO solve this simple problem by a simple way.
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525
|
| |



 .
.