Question 1206230: A vector has magnitude 6.0 units due east, vector B points due north. Find
a) the magnitude of B if A+B points 60° north of east?
b) the magnitude of A+B
Answer by ikleyn(52817)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A vector has magnitude 6.0 units due east, vector B points due north. Find
a) the magnitude of B if A+B points 60° north of east?
b) the magnitude of A+B
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In this post, first sentence is incorrect. Instead of " A vector has magnitude 6.0 units due east, . . . "
should be " Vector A has magnitude 6.0 units due east, . . . ".
It may seems like a small microscopic thing, but in Math every word matters, and the order
of the words does matters, too. Wrong order of words makes the post non-sensical.
So, I will solve the problem, edited this way.
(a) Since in the coordinate plane vector A is vertical and vector B is horizontal,
vector A+B has x-component Ax = 6 = |A|, the magnitude of vector A,
and has y-component |B|, the magnitude of vector B.
Since tan(60°) =  , it implies that , it implies that 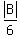 = =  .
From this equation, we get |B| = .
From this equation, we get |B| =  = 10.3923 (rounded).
It gives the ANSWER to question (a) : the magnitude of vector B is = 10.3923 (rounded).
It gives the ANSWER to question (a) : the magnitude of vector B is  = 10.3923 (rounded).
(b) Now we know that x-component of vector A+B is the same as x-component of vector A, i.e. 6,
and we know that y-component of vector A+B is the same as y-component of vector B, i.e. = 10.3923 (rounded).
(b) Now we know that x-component of vector A+B is the same as x-component of vector A, i.e. 6,
and we know that y-component of vector A+B is the same as y-component of vector B, i.e.  .
Hence, the magnitude of A+B is .
Hence, the magnitude of A+B is 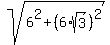 = = 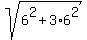 = = 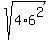 = 2*6 = 12.
It gives the ANSWER to question (b) : the magnitude of A+B is 12. = 2*6 = 12.
It gives the ANSWER to question (b) : the magnitude of A+B is 12.
Solved.
|
|
|