SOLUTION: five different positive integers added two at a time give the following sums:16,20,22,23,25,28,29,30,34 and 37.Find the product of the five integers.

1.  Let the numbers be a < b < c < d < e   (in this order/ordering).

    Four pair-wise sums of "a" with four other numbers are among the given set {16,20,22,23,25,28,29,30,34,37}.

    Four pair-wise sums of "b" with four other numbers are among the given set {16,20,22,23,25,28,29,30,34,37}.

    Four pair-wise sums of "c" with four other numbers are among the given set {16,20,22,23,25,28,29,30,34,37}.

    Four pair-wise sums of "d" with four other numbers are among the given set {16,20,22,23,25,28,29,30,34,37}.

    Four pair-wise sums of "e" with four other numbers are among the given set {16,20,22,23,25,28,29,30,34,37}.


    Therefore, if we sum up all the given numbers, we will get 4*(a+b+c+d+e):

    4*(a + b + c + d + e) = 16+20+22+23+25+28+29+30+34+37 = 264.

    It implies that 

    a + b + c + d + e = 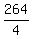 = 66.   (1)


2.  Further, 16 is the sum of the two smallest numbers: 16 = a + b.   (2)

             37 is the sum of the two largest numbers:  37 = d + e.   (3)

    It implies (by subtracting (2) and (3) from (1)) that c = 66 - 16 - 37 = 13.

    So, we just found one of the five numbers, namely, the middle number c = 13.

    
3.  OK. Let's continue our analysis.

    So, the two smallest numbers a and b give the sum of 16, and the third number is 13.

    It means that the next sum, 20 (see the condition) is  a+c.
    It can not be nothing else. (Because b + c must be just greater than a + c).
    If  a + c = 20  and  c = 13, then  a = 20 - 13 = 7. 
    It implies b = 16-7 = 9.

    So, the first three numbers are  a = 7, b = 9  and  c = 13.


4.  OK. Now we can make the similar analysis from the other end.

    So, the two largest numbers d and e give the sum of 37, and the third number in the descending order is 13.

    It means that the next from the largest sum, 34 (see the condition) is  e+c.
    It can not be nothing else. (Because d + c is just less than e + c).
    If  e + c = 34  and  c = 13, then  e = 34 - 13 = 21. 
    It implies d = 37-21 = 16.


5.  Thus the numbers are 7, 9, 13, 16 and 21.


    Then their product is 275184.