Question 954704: Provide all the value(s) of theta that satisfy the equation, csc theta = 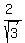 . .
Thank you
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! csc(theta) = 2 / sqrt(3) means that sin(theta) = sqrt(3)/2
this is because sin(theta) = 1 / csc(theta and csc(theta) = 1 / sin(theta)
if 1 / sin(theta) = 2 / sqrt(3), then solve for sin(theta) to get:
sin(theta) = sqrt(3)/2.
arcsin(sqrt(3)/2) = 60 degrees.
your angle in the first quadrant is equal to 60 degrees.
the sine is positive.
sine is positive in the first and second quadrants, so your angle could be equal to 60 degrees and it could be equal to 180 - 60 = 135 degrees.
since cosecant carries the same sign as sine, then your angle is still in the first quadrant and the second quadrant.
it cannot be in the third quadrant or the fourth quadrant because sine, and therefore cosecant, is negative in the third and fourth quadrant.
also, you can have an infinite number of angles that have the same sine and the same cosecant.
those angles will be:
60 plus or minus 360 degrees.
135 plus or minus 360 degrees.
if you let k be a non-negative integer, then the general formula for your angles would be:
60 degrees plus or minus k * 360 for k from 0 to infinity.
135 degrees plus or minus k * 360 for k from 0 to infinity.
that will get you all the positive sines and all the angles that have a sine of sqrt(3) / 2 and have a cosecant of 2 / sqrt(3).
the graph of your equation is shown below, the first graph is for sine and the second graph is for cosecant.
only 3 cycles of the angles are shown, but the graph goes on forever in both directions because it is cyclical with one cycle being completed every 360 degrees.


|
|
|