Question 934401: A paddle wheel has a 10ft. diameter. At t=0, Jenn notices a weed stuck to the top of the paddle, which is 8ft above the surface of the water. It takes 4 seconds for the paddle to return to the same position. Find a function that will model the height of the weed above the water at any time (t).
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i believe your equation is going to be:
y = 5cos(90x)+3
your calculator, if you have one that graphs, should be set to degree mode.
the basic equation that is used is y = a * cos(b*(x-c) + d
a is the amplitude.
b is the frequency.
c is the horizontal displacement.
d is the vertical displacement.
c is equal to 0 because there is no horizontal displacement.
if a is equal to 1 and b is equal to 1 and d is equal to 0 and c is equal to 0, the equation becomes:
y = cos(x).
the cos(x) function is equal to 1 when x is equal to 0 degrees and is equal to 0 when x is equal to 180 degrees
that function looks like this:
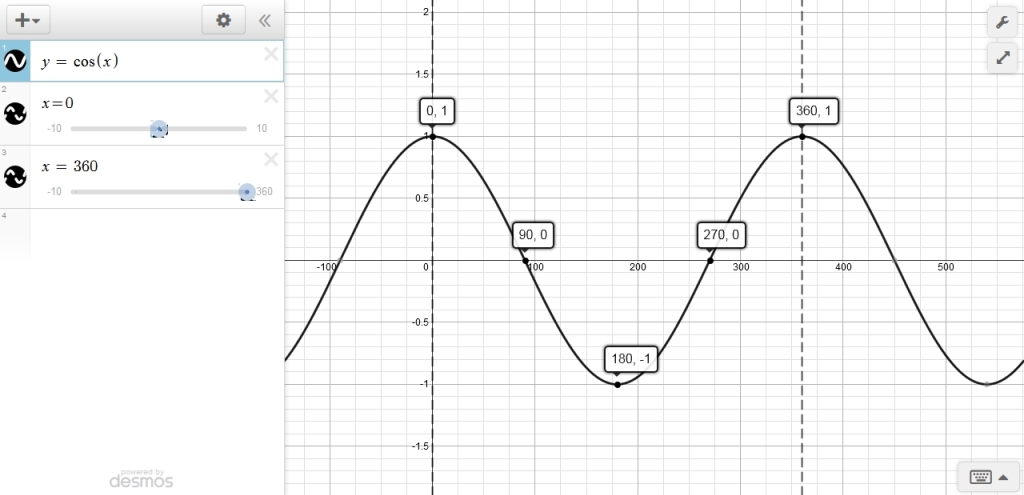
the period is equal to 360 degrees.
we want the period to be equal to 4 degrees in order to simulate 4 seconds where each degree is equal to 1 second.
the formula for frequency is that frequency = 360 / period.
the formula for period is that period = 360 / frequency.
we want to find the frequency, so we use the frequency formula.
we get frequency = 360 / 4 which is equal to 90.
if we make frequency equal to 90, than the period of the cosine function, where it goes through one complete cycle, will be 4.
our formula becomes:
y = cos(90x) with nothing else changed.
the graph of that equation looks like this:
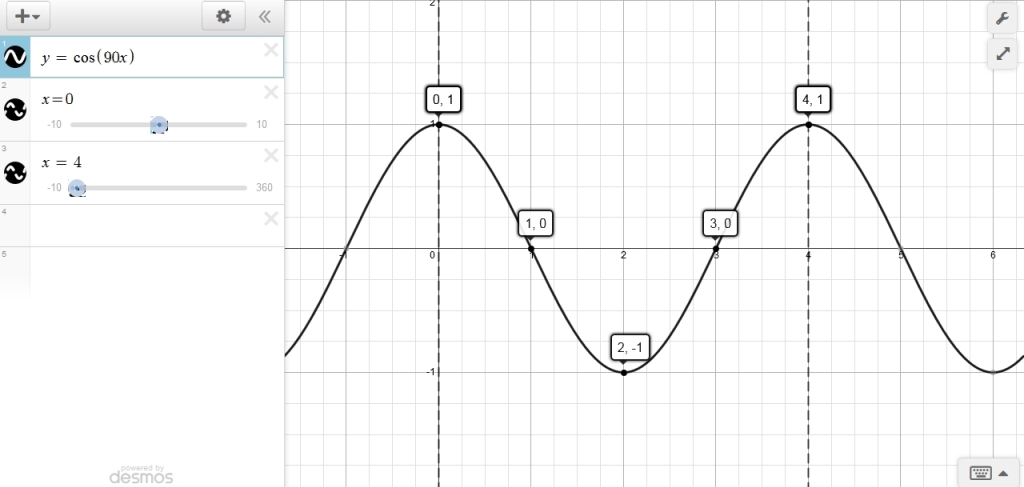
that looks a lot like the last graph only the period is equal to 4 rather than 360.
the diameter of the paddle wheel is equal to 10 which means the radius is equal to 5.
we want the graph of the paddle wheel to have a high point of 5 and a low point of 5 rather than a high point of 1 and a low point of 1.
we make our a factor in the equation of y = a * cos(b * (x-c)) + d equal to 5 and keep our b factor to 90 and our equation becomes:
y = 5 * cos(90 * x)
the graph of that equation looks like this:
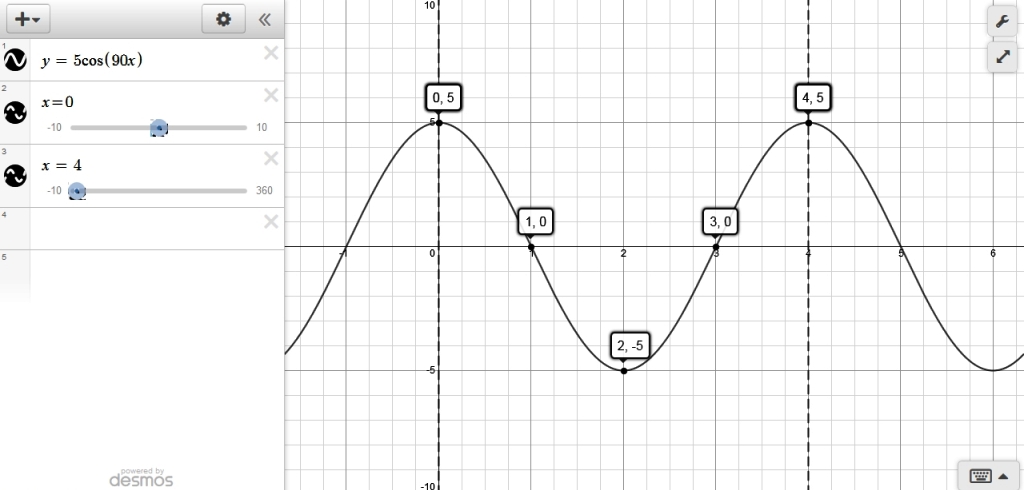
we're almost there.
we want the height of the weed that is stuck to the paddle to be 8 feet high above the water line when the number of seconds is 0.
we have to add 3 to the height of out graph because 5 + 3 will be equal to 8.
we do this by changing d from 0 to 3.
our equation now becomes:
y = 5 * cos(90 * x) + 3
that graph looks like this:
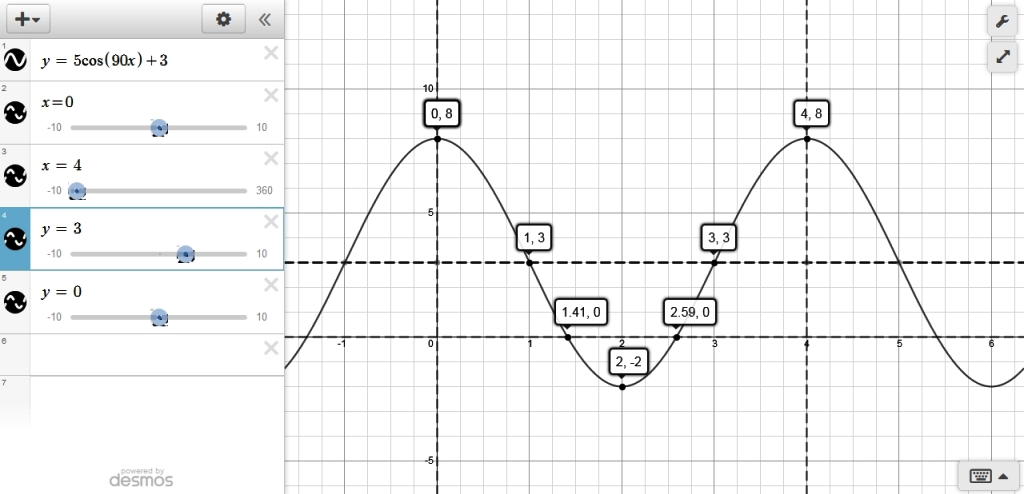
x represents the seconds.
the center of the paddle wheel is at y = 3
the radius of the paddle wheel is equal to 5.
the water line is at y = 0
when x = 0, y = 8 feet high above the water line which is what we want.
when x = 4, the cycle completes and the height of the weed is 8 again.
in between are the different intermediate cycles of the function of y = 5 * cos(90 * x) + 3
they are:
0 seconds = 8
1 second = 3
2 seconds = -2
3 seconds = 3
4 seconds = 8
y = 3 is the center line of the cosine function.
it fluctuates plus 5 from that and - 5 from that.
it is also the center of the paddle wheel.
it's the hub that the paddle wheel revolves around.
y = 0 is the water line.
anything above that is in the air above the water.
anything below that is in the water.
the weed stuck on the paddle wheel goes round and round every 4 seconds.
it's high point is 8 feet above the water line.
it's low point is 2 feet below the water line.
using this equation, we can find the height of the weed any number of seconds into the revolution of the paddle wheel.
simply replace x in the equation and solve for y using your calculator in degree mode.
the equation is, once again, y = 5 * cos(90 * x) + 3
|
|
|