To find the reference number.
1. Sometimes you do nothing, because the number IS the reference number
2. Sometimes you subtract from  3. Sometimes you subtract
3. Sometimes you subtract  from the number
4. Sometimes you subtract the number from
from the number
4. Sometimes you subtract the number from  5. Sometimes you have to subtract
5. Sometimes you have to subtract  1 or more time and then do one of
1,2,3,or 4
5. When the number is negative sometimes you just change the sign of the number.
6. Sometimes you subtract the negative number from
1 or more time and then do one of
1,2,3,or 4
5. When the number is negative sometimes you just change the sign of the number.
6. Sometimes you subtract the negative number from  7. Sometimes you subtract
7. Sometimes you subtract  from the number.
8. Sometimes you subtract the number from
from the number.
8. Sometimes you subtract the number from 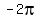 etc. etc. etc.
To find the reference number, you MUST draw the arc on the unit circle because
it's different for every quadrant and direction of rotation. if it is more than
etc. etc. etc.
To find the reference number, you MUST draw the arc on the unit circle because
it's different for every quadrant and direction of rotation. if it is more than
 then you must subtract
then you must subtract  for every revolution. You can't just
learn a bunch of rules. There are too many. You have to draw the arc each
time. Positive numbers are rotated counter-clockwise and negative numbers are rotated clockwise.
Find the reference number of t = 11π/7 and t = 11π/5?
t = 11π/7
t = 11π/5
for every revolution. You can't just
learn a bunch of rules. There are too many. You have to draw the arc each
time. Positive numbers are rotated counter-clockwise and negative numbers are rotated clockwise.
Find the reference number of t = 11π/7 and t = 11π/5?
t = 11π/7
t = 11π/5


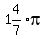
 is positive so it's the red counter-clockwise arc
around the unit circle from (1,0). The red arc extends
is positive so it's the red counter-clockwise arc
around the unit circle from (1,0). The red arc extends 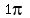 from (1,0) to (-1,0) and since it's
from (1,0) to (-1,0) and since it's 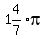 ,
it's
,
it's  of that arc more, which is a tad more as the red arc we
see below. Then the green arc is the reference number.
of that arc more, which is a tad more as the red arc we
see below. Then the green arc is the reference number.
 Since it's
Since it's  units all the way around the unit circle and the
red arc is
units all the way around the unit circle and the
red arc is  , the green arc is
, the green arc is  Answer:
Answer:  is the reference number.
-----------
is the reference number.
-----------
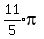

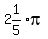
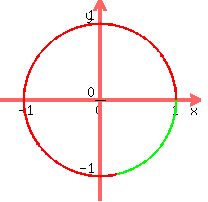
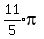 is positive and therefore it goes counter-clockwise.
It's also more than
is positive and therefore it goes counter-clockwise.
It's also more than  , so it's more than 1 complete revolution. In
fact it goes all the way around the unit circle and overlaps
, so it's more than 1 complete revolution. In
fact it goes all the way around the unit circle and overlaps  of the way
past (1,0) toward (-1,0).
It's the red counter-clockwise arc below that goes around the unit circle from
(1,0) past (-1,0) on around back to (1,0) and overlaps
of the way
past (1,0) toward (-1,0).
It's the red counter-clockwise arc below that goes around the unit circle from
(1,0) past (-1,0) on around back to (1,0) and overlaps  of the way
past where it started at (1,0). Then the green arc is the reference number.
It's the arc that equals the amount which the red arc goes past 1 revolution
or
of the way
past where it started at (1,0). Then the green arc is the reference number.
It's the arc that equals the amount which the red arc goes past 1 revolution
or 
 Since it's
Since it's  units all the way around the unit circle and the
red arc is
units all the way around the unit circle and the
red arc is 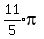 , the green arc is
, the green arc is  Answer:
Answer: 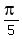 is the reference number.
Edwin
is the reference number.
Edwin