Question 916978: David's garden plot is in the shape of a quadrilateral. If the corner points are A, B, C and D then the angles at A and C are 120 degrees and 60 degrees respectively. AD = 16m, BC = 25m, and (DC) is 5m longer than (AB). A fence runs around the entire boundary of the plot. How long is the fence?
Found 2 solutions by catcat1, Bakr.R:
Answer by catcat1(1)   (Show Source): (Show Source):
Answer by Bakr.R(8)   (Show Source): (Show Source):
You can put this solution on YOUR website! To start at first, we may lay out a diagram by the given information:
 . .
Diagram source: Haesemathematics
The question requires us to find the total length of the fence, they provide us with two angles at opposing sides, and a definite side along with each angle, and that allows us to cut the quadrilateral into two triangles without affecting any values:
 . .
Now that we have cut the shape into two triangles, trigonometric calculations (methods) may be used.
Two sides are unknown, but in the question it is mentioned that the length of DC is 5 m longer than AB, and through that we may deduce an expression for each side, let x be the unknown value:
 . .
In each triangle, there is only one angle and a definite side, with two unknowns (two sides), and so no rule may be used to solve for the unknown, but, the two triangles have something in common, being that two triangles share one side, being equal for both, which is the length of DB.
From having DB the common side, we can deduce for each triangle an equation, using the cosine rule 
For Triangle ABD we may deduce the equation: 
For Triangle BCD we may deduce the equation: 
It is apparent now, that we can equal these two equations and find the unknown, but to make the method more simple, let us simplify each equation first.
The equation for triangle ABD;

 cos(120)=-1/2 or -0.5 cos(120)=-1/2 or -0.5
 Now we have a simplified equation. Now we have a simplified equation.
The equation of triangle BCD:

 cos(60)=1/2 or 0.5 cos(60)=1/2 or 0.5

 Now we have a simplified equation for both triangles. Now we have a simplified equation for both triangles.
From here, we can also (obviously) deduce that  , and so through that, using both of the simplified equations: , and so through that, using both of the simplified equations:
 And now we further simplify and solve to find the value of the unknown. And now we further simplify and solve to find the value of the unknown.



Now that we've found a value for x, we may solve the problem by substituting it into the equation for finding the total length of the fence, by finding the perimeter of the quadrilateral:
 or or 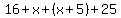
 rounded to hundredth d.p. rounded to hundredth d.p.
|
|
|